
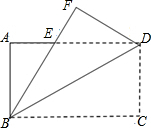
 如图所示,把矩形ABCD沿对角线BD折叠,点C落在点F处,若AB=12cm,BC=16cm.
如图所示,把矩形ABCD沿对角线BD折叠,点C落在点F处,若AB=12cm,BC=16cm.分析 (1)由矩形的性质和折叠的性质得出∠EDB=∠DBE,证出BE=DE,设AE=xcm,则BE=DE=(16-x)cm,在Rt△ABE中,根据勾股定理得出方程,解方程即可;
(2)根据勾股定理得到BE=$\sqrt{A{E}^{2}+A{B}^{2}}$=$\frac{25}{2}$,由于四边形ABCD是矩形,得到∠C=90°CD=AB=12,由折叠的性质得DF=CD=12,∠F=∠C=90°,于是得到结果.
解答 解:(1)∵四边形ABCD是矩形,
∴AD=BC=16cm,∠A=90°,AD∥BC,
∴∠EDB=∠DBC,
由折叠的性质得:∠DBE=∠DBC,
∴∠EDB=∠DBE,
∴BE=DE,
设AE=xcm,
则BE=DE=(16-x)cm,
在Rt△ABE中,根据勾股定理得:AE2+AB2=BE2,
即x2+122=(16-x)2,
解得:x=$\frac{7}{2}$,
∴AE=$\frac{7}{2}$cm;
(2)∵BE=$\sqrt{A{E}^{2}+A{B}^{2}}$=$\frac{25}{2}$,
∵四边形ABCD是矩形,
∴∠C=90°CD=AB=12,
由折叠的性质得DF=CD=12,∠F=∠C=90°,
∴S△BDE=$\frac{1}{2}$BE•DF=$\frac{1}{2}$×$\frac{25}{2}×12$=75cm2,
∴重合部分的面积是75cm2.
点评 本题考查了矩形的性质、翻折变换的性质、勾股定理;熟练掌握翻折变换和矩形的性质,并能进行推理计算是解决问题的关键.


 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | y2>y1>y3 | B. | y1>y2>y3 | C. | y3>y2>y1 | D. | y1>y3>y2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,将Rt△ABC绕直角顶点顺时针旋转90°,得到△A′B′C,连接AA′,若∠1=22°,则∠B的度数是( )
如图,将Rt△ABC绕直角顶点顺时针旋转90°,得到△A′B′C,连接AA′,若∠1=22°,则∠B的度数是( )| A. | 67° | B. | 62° | C. | 82° | D. | 72° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
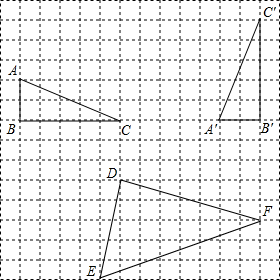 在如图所示的方格图中,每个小正方形的顶点成为“格点”,且每个小正方形的边长均为1个长度单位,以格点为顶点的图形叫做“格点图形”,根据图形解决下列问题:
在如图所示的方格图中,每个小正方形的顶点成为“格点”,且每个小正方形的边长均为1个长度单位,以格点为顶点的图形叫做“格点图形”,根据图形解决下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com