


 ,将将△BAC沿射线A´C´方向平移m个单位长度,使BC边经过点D,求m的值.
,将将△BAC沿射线A´C´方向平移m个单位长度,使BC边经过点D,求m的值. -
-
 A´C´=
A´C´= ,△DHC∽△BAC,根据相似三角形的性质可得CH=
,△DHC∽△BAC,根据相似三角形的性质可得CH= ,即可求得结果.
,即可求得结果. A´C´=
A´C´= ,△DHC∽△BAC,可得CH=
,△DHC∽△BAC,可得CH= .
. -
- .
.


科目:初中数学 来源:不详 题型:解答题
 放置于矩形
放置于矩形 上,
上, 三角板的一个
三角板的一个 角的顶点放在
角的顶点放在 处, 且直角边
处, 且直角边 在矩形内部绕点
在矩形内部绕点 旋转,在旋转过程中
旋转,在旋转过程中 与
与 交于点
交于点 .
.  与
与 的有何数量关系?并说明理由;
的有何数量关系?并说明理由; 为等腰三角形,若存在,求出
为等腰三角形,若存在,求出 的长,若不存在,说明理由.
的长,若不存在,说明理由. 为边在矩形内部作正方形
为边在矩形内部作正方形 ,直角边
,直角边 所在的直线交
所在的直线交 于
于 ,交
,交 于
于 .设
.设 写出
写出 关于
关于 的函数关系式.
的函数关系式.
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
 中,
中,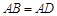 ,
,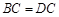 ,
,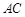 与
与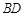 相交于点
相交于点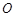 ,下列判断正确的有 .(填序号).
,下列判断正确的有 .(填序号).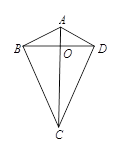
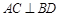 ;
;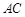 、
、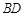 互相平分;
互相平分;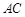 平分
平分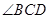 ;
;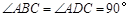 ;
; 的面积为
的面积为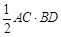 .
.查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.12米 | B.13米 | C.14米 | D.15米 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com