
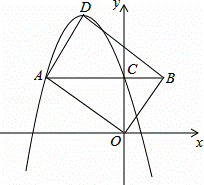
��ͼ����֪��ƽ��ֱ������ϵxOy�У�O������ԭ�㣬������y=��x2+bx+c��c��0���Ķ���ΪD����y��Ľ���ΪC������C��CA��x�ύ�������ڵ�A����AC�ӳ�����ȡ��B��ʹBC=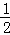 AC������OA��OB��BD��AD��
AC������OA��OB��BD��AD��
��1������A�������ǣ���4��4��
����b��c��ֵ��
�����ж��ı���AOBD����״����˵�����ɣ�
��2���Ƿ���������ĵ�A��ʹ���ı���AOBD�Ǿ��Σ������ڣ���ֱ��д��һ�����������ĵ�A�����ꣻ������ �ڣ���˵�����ɣ�
�ڣ���˵�����ɣ�
�⣺��1��
�١�AC��x�ᣬA������Ϊ����4��4�������C�������ǣ�0��4��
��A��C����y�T��x2+bx+c�ã� ��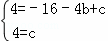 �����
�����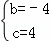 ��
��
���ı���AOBD��ƽ���ı��Σ��������£�
�ɢٵ������ߵĽ���ʽΪy�T��x2��4x+4���ඥ��D������Ϊ����2��8����
��D����DE��AB�ڵ�E����DE=OC=4��AE=2��
��AC=4����BC=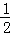 AC=2����AE=BC����AC��x�ᣬ���AED=��BCO=90�㣬
AC=2����AE=BC����AC��x�ᣬ���AED=��BCO=90�㣬
���AED�ա�BCO����AD=BO����DAE=��BCO����AD��BO��
���ı���AOBD��ƽ���ı��Σ�
��2�����ڣ���A����������ǣ���2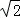 ��2����2
��2����2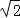 ��2��
��2��
Ҫʹ�ı���AOBD�Ǿ��Σ������AOB=��BCO=90�㣬
�ߡ�ABO=��OBC�����ABO�ס�OBC����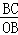 =
=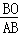 ��
��
�֡�AB=AC+BC=3BC����OB=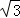 BC��
BC��
����Rt��OBC�У����ݹ��ɶ����ɵã�OC=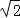 BC��AC=
BC��AC=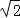 OC��
OC��
��C������������y�ύ�㣬��OC=c��
��A�� ������
����Ϊ��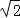 c��c�����ඥ�������
c��c�����ඥ�������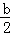 =
= c��b=
c��b=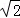 c��
c��
�߽�A�����ɵ�c=��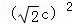 +
+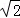 c•
c•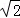 c+c��
c+c��
�������Ϊ��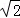 c��������Ϊc���ɣ���c=2��
c��������Ϊc���ɣ���c=2��
��A���������Ϊ��2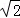 ��2�����ߣ���2
��2�����ߣ���2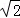 ��2����
��2����


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
���������������������( )
A�����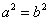 ����ô
����ô
B���Խ����ഹֱ���ı���������
C����תǰ�������ͼ�Σ���Ӧ�������߶����
D���߶δ�ֱƽ�����ϵĵ㵽�����߶������˵�ľ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
4.�ɼ�����С��ͬ����������ɵļ���ͼ����ͼ��ʾ�������ĸ���ͼ�� ��
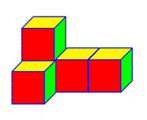


A B



C  D
D
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
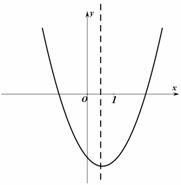
���κ���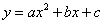 ͼ����ͼ��ʾ��������ȷ�ĸ���Ϊ�� ��
ͼ����ͼ��ʾ��������ȷ�ĸ���Ϊ�� ��
 ��
�� 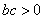
�� 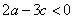
�� 
��  ��������
�������� ��
��
�� 
�� �� ʱ��
ʱ�� ��
�� �������С
�������С
A. 2 B. 3 C. 4 D. 5
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
ij�����12����Ա���������±� ��ʾ��
��ʾ��
| ���䣨�꣩ | 18 | 19 | 20 | 21 |
| ���� | 5 | 4 | 1 | 2 |
����12����Ա�����������ƽ�����ֱ���
A��18��19 B��19��19 C��18�� D��19��
D��19��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
С����ͬѧһ��ȥ���Σ�����һ�ô���б����һС�����ϣ�����֪�����ж����������������Ǻ;���.��ͼ�����ڵ�C�������AB����A������Ϊ30�㣬����CB����������н�10�����D�������AB����A������Ϊ45�㣬�ֲ����AB��б�ǡ�1=75��.
��1����5�֣���AD�ij�. ��2����4�֣�������AB.

��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com