
【题目】如图,正方形![]() 的顶点
的顶点![]() ,
,![]() 分别在
分别在![]() 轴和
轴和![]() 轴上与双曲线
轴上与双曲线![]() 恰好交于
恰好交于![]() 的中点
的中点![]() ,若
,若![]() ,则
,则![]() 的值为( )
的值为( )

A.6B.8C.12D.16
【答案】C
【解析】
过点B作x轴的平行线,过点A,C分别作y轴的平行线,两线相交于M,N,证明△ABM≌△BCN,可得BN=AM=2a,CN=BM=a,所以点C坐标为(2a,a),BC的中点E的坐标为(a,1.5a),把点E代入双曲线![]() 可得a的值,进而得出S△ABO的值.
可得a的值,进而得出S△ABO的值.
如图,过点B作x轴的平行线,过点A,C分别作y轴的平行线,两线相交于M,N,
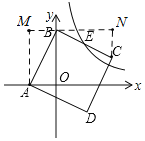
∵四边形ABCD为正方形,
∴∠ABC=90°,AB=BC,
∴∠ABM=90°-∠CBN=∠BCN,
∵∠M=∠N=90°,
∴△ABM≌△BCN(AAS),
∵OB=2OA,
∴设OA=a,OB=2a,
则BN=AM=2a,CN=BM=a,
∴点C坐标为(2a,a),
∵E为BC的中点,B(0,2a),
∴E(a,1.5a),
把点E代入双曲线![]() 得1.5a2=18,a2=12,
得1.5a2=18,a2=12,
∴S△ABO=![]() a2a=12,
a2a=12,
故选:C.


科目:初中数学 来源: 题型:
【题目】已知:梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分别交射线
分别交射线![]() 、射线
、射线![]() 于点
于点![]() 、
、![]() .
.
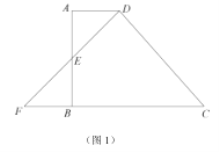
(1)当点![]() 为边
为边![]() 的中点时(如图1),求
的中点时(如图1),求![]() 的长:
的长:
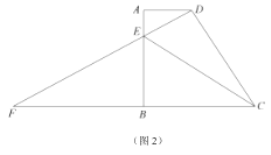
(2)当点![]() 在边
在边![]() 上时(如图2),联结
上时(如图2),联结![]() ,试问:
,试问:![]() 的大小是否确定?若确定,请求出
的大小是否确定?若确定,请求出![]() 的正切值;若不确定,则设
的正切值;若不确定,则设![]() ,
,![]() 的正切值为
的正切值为![]() ,请求出
,请求出![]() 关于
关于![]() 的函数解析式,并写出定义域;
的函数解析式,并写出定义域;
(3)当![]() 的面积为3时,求
的面积为3时,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
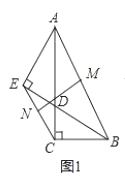
【题目】如图1,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在边
在边![]() 上,连接
上,连接![]() ,过
,过![]() 作
作![]() 的垂线交
的垂线交![]() 的延长线于点
的延长线于点![]() .
.
(1)若![]() ,
,![]() 分别为线段
分别为线段![]() ,
,![]() 的中点,如图1,求证:
的中点,如图1,求证:![]() ;
;
(2)如图2,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,求证:
,求证:![]() ;
;
(3)如图3,以![]() 为一边作一个角等于
为一边作一个角等于![]() ,这个角的另一边与
,这个角的另一边与![]() 的延长线交于
的延长线交于![]() 点,
点,![]() 为
为![]() 的中点,连接
的中点,连接![]() ,求证:
,求证:![]() .
.
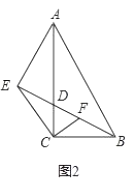
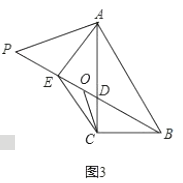
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,以
,以![]() 为直径作圆
为直径作圆![]() ,分别交
,分别交![]() 于点
于点![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() 交线段
交线段![]() 于点
于点![]() .
.
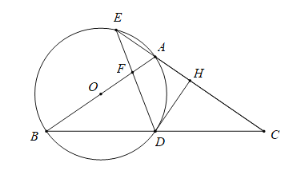
(1)求证:![]() 是圆
是圆![]() 的切线;
的切线;
(2)若![]() 为
为![]() 的中点,求
的中点,求![]() 的值;
的值;
(3)若![]() ,求圆
,求圆![]() 的半径.
的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】规定:[x]表示不大于x 的最整数,(x) 表示不小于x的最小整数,[x) 表示最接近x的整数(x≠n+0.5,n为整数),例如:[2.3]=2,(2.3)=3,[2.3)=2,则下列说法正确的是__________(写出所有正确说法).
①当x=1.7时,[x]+(x)+[x)=6;
②当x=-2.1时,[x]+(x)+[x)=-7;
③方程4[x]+3(x)+[x)=11的解为1<x<1.5;
④当-1<x<1时, 函数y=[x]+(x)+x 的图像y=4x 的图像有两个交点.
【答案】②③
【解析】分析:(1)根据题目中给的计算方法代入计算后判定即可;(2)根据题目中给的计算方法代入计算后判定即可;(3)根据题目中给的计算方法代入计算后判定即可;(4)结合x的取值范围,分类讨论,利用题目中给出的方法计算后判定即可.
详解:
①当x=1.7时,
[x]+(x)+[x)
=[1.7]+(1.7)+[1.7)=1+2+2=5,故①错误;
②当x=﹣2.1时,
[x]+(x)+[x)
=[﹣2.1]+(﹣2.1)+[﹣2.1)
=(﹣3)+(﹣2)+(﹣2)=﹣7,故②正确;
③当1<x<1.5时,
4[x]+3(x)+[x)
=4×1+3×2+1
=4+6+1
=11,故③正确;
④∵﹣1<x<1时,
∴当﹣1<x<﹣0.5时,y=[x]+(x)+x=﹣1+0+x=x﹣1,
当﹣0.5<x<0时,y=[x]+(x)+x=﹣1+0+x=x﹣1,
当x=0时,y=[x]+(x)+x=0+0+0=0,
当0<x<0.5时,y=[x]+(x)+x=0+1+x=x+1,
当0.5<x<1时,y=[x]+(x)+x=0+1+x=x+1,
∵y=4x,则x﹣1=4x时,得x=![]() ;x+1=4x时,得x=
;x+1=4x时,得x=![]() ;当x=0时,y=4x=0,
;当x=0时,y=4x=0,
∴当﹣1<x<1时,函数y=[x]+(x)+x的图象与正比例函数y=4x的图象有三个交点,故④错误,
故答案为:②③.
点睛:本题是阅读理解题,前三问比较容易判定,根据题目所给的方法判定即可;第四问较难,结合x的取值范围分情况讨论即可.
【题型】填空题
【结束】
19
【题目】先化简再求值: ![]() ,其中
,其中![]() ,
, ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】银泰百货名创优品店购进600个钥匙扣,进价为每个8元,第一周以每个12元的价格售出200个,第二周若按每个12元的价格销售仍可售出200个,但商店为了适当增加销量,决定降价销售.据市场调查,单价每降低1元,可多售出50个,但售价不得低于进价,单价降低![]() 元销售,销售一周后,商店对剩余钥匙扣清仓处理,以每个6元的价格全部售出.
元销售,销售一周后,商店对剩余钥匙扣清仓处理,以每个6元的价格全部售出.
(1)如果这批钥匙扣共获利1050元,那么第二周每个钥匙扣的销售价格为多少元?
(2)这次降价活动,1050元是最高利润吗?若是,说明理由;若不是,求出最高利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】.Rt△ABC中,已知∠C=90°,∠B=50°,点D在边BC上,BD=2CD(图4).把△ABC绕着点D逆时针旋转m(0<m<180)度后,如果点B恰好落在初始Rt△ABC的边上,那么m=_________![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场为了吸引顾客,设立了一个可以自由转动的转盘,如图所示,并规定:顾客消费200元(含200元)以上,就能获得一次转动转盘的机会,如果转盘停止后,指针正好对准九折、八折、七折区域,顾客就可以获得此项优惠,如果指针恰好在分割线上时,则需重新转动转盘.
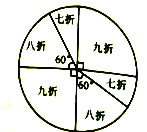
(1)某顾客正好消费220元,他转一次转盘,他获得九折、八折、七折优惠的概率分别是多少?
(2)某顾客消费中获得了转动一次转盘的机会,实际付费168元,请问他消费所购物品的原价应为多少元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若一个三角形一条边的平方等于另两条的乘积,我们把这个三角形叫做比例三角形.
(1)已知![]() 是比例三角形,
是比例三角形,![]() ,
,![]() ,请直接写出所有满足条件的
,请直接写出所有满足条件的![]() 的长;
的长;
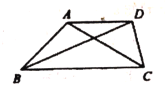
(2)如图,在四边形![]() 中,
中,![]() ,对角线
,对角线![]() 平分
平分![]() ,
,![]() .求证:
.求证:![]() 是比例三角形;
是比例三角形;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com