
【题目】若一个三角形一条边的平方等于另两条的乘积,我们把这个三角形叫做比例三角形.
(1)已知![]() 是比例三角形,
是比例三角形,![]() ,
,![]() ,请直接写出所有满足条件的
,请直接写出所有满足条件的![]() 的长;
的长;
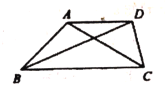
(2)如图,在四边形![]() 中,
中,![]() ,对角线
,对角线![]() 平分
平分![]() ,
,![]() .求证:
.求证:![]() 是比例三角形;
是比例三角形;
【答案】(1)当AC=![]() 或
或![]() 或
或![]() 时,△ABC是比例三角形;(2)见解析
时,△ABC是比例三角形;(2)见解析
【解析】
(1)根据比例三角形的定义,分AB2=BCAC、BC2=ABAC、AC2=ABBC三种情况分别代入计算可得;
(2)先证△ABC∽△DCA得CA2=BC·AD,再由∠ADB=∠CBD=∠ABD知AB=AD即可得.
(1)∵△ABC是比例三角形,且AB=2、BC=3,
①当AB2=BC·AC时,得:4=3AC,解得:AC=![]() ;
;
②当BC2=AB·AC时,得:9=2AC,解得:AC=![]() ;
;
③当AC2=AB·BC时,得:AC2=6,解得:AC=![]() (负值舍去);
(负值舍去);
所以当AC=![]() 或
或![]() 或
或![]() 时,△ABC是比例三角形;.
时,△ABC是比例三角形;.
(2)∵AD//BC,
∴∠ACB=∠CAD,
又∵∠BAC=∠ADC,
∴△ABC∽△DCA,
∴![]() ,即CA2=BC·AD,
,即CA2=BC·AD,
∵AD∥BC,
∴∠ADB=∠CBD,
∵BD平分∠ABC,
∴∠ABD=∠CBD,
∴∠ADB=∠ABD,
∴AB=AD,
∴CA2=BC·AB,
∴△ABC是比例三角形.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点P、D分别是BC、AC边上的点,且∠APD=∠B.
(1)求证:AC·CD=CP·BP;
(2)若AB=10,BC=12,当PD∥AB时,求BP的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
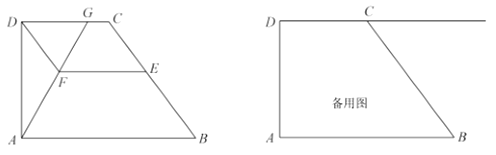
【题目】如图,已知梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 是边
是边![]() 上一点,过
上一点,过![]() 、
、![]() 分别作
分别作![]() 、
、![]() 的平行线交于点
的平行线交于点![]() ,联结
,联结![]() 并延长,与射线
并延长,与射线![]() 交于点
交于点![]() .
.
(1)当点![]() 与点
与点![]() 重合时,求
重合时,求![]() 的值;
的值;
(2)当点![]() 在边
在边![]() .上时,设
.上时,设![]() ,求
,求![]() 的面积;(用含
的面积;(用含![]() 的代数式表示)
的代数式表示)
(3)当![]() 时,求
时,求![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:初中数学 来源: 题型:
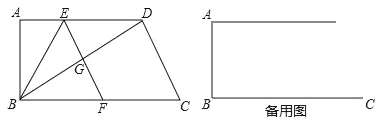
【题目】如图,在四边形![]() 中
中![]() ,
,![]() ,
,![]() ,点
,点![]() 为边
为边![]() 上一点,将
上一点,将![]() 沿
沿![]() 翻折,点
翻折,点![]() 落在对角线
落在对角线![]() 上的点
上的点![]() 处,连接
处,连接![]() 并延长交射线
并延长交射线![]() 于点
于点![]() .
.
(1)如果![]() ,求
,求![]() 的长;
的长;
(2)当点![]() 在边
在边![]() 上时,连接
上时,连接![]() ,设
,设![]() ,求
,求![]() 关于
关于![]() 的函数关系式并写出
的函数关系式并写出![]() 的取值范围;
的取值范围;
(3)连接![]() ,如果
,如果![]() 是等腰三角形,求
是等腰三角形,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
在数学课上,老师提出如下问题:
尺规作图:作Rt△ABC,使其斜边AB=c,一条直角边BC=a.
已知线段a,c如图.

小芸的作法如下:
① 取AB=c,作AB的垂直平分线交AB于点O; ② 以点O为圆心,OB长为半径画圆;
③ 以点B为圆心,a长为半径画弧,与⊙O交于点C;④ 连接BC,AC.
则Rt△ABC即为所求.老师说:“小芸的作法正确.”
请回答:小芸的作法中判断∠ACB是直角的依据是________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
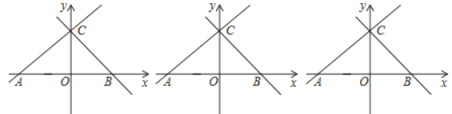
【题目】如图,已知一次函数![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,一次函数
,一次函数![]() 经过点
经过点![]() 与
与![]() 轴交于点.
轴交于点.
(1)求直线![]() 的解析式;
的解析式;
(2)点![]() 为
为![]() 轴上方直线
轴上方直线![]() 上一点,点
上一点,点![]() 为线段
为线段![]() 的中点,点
的中点,点![]() 为线段
为线段![]() 的中点,连接
的中点,连接![]() ,取
,取![]() 的中点
的中点![]() ,射线
,射线![]() 交
交![]() 轴于点
轴于点![]() ,点
,点![]() 为线段
为线段![]() 的中点,点
的中点,点![]() 为线段
为线段![]() 的中点,连接
的中点,连接![]() ,求证:
,求证:![]() ;
;
(3)在(2)的条件下,延长![]() 至
至![]() ,使
,使![]() ,连接
,连接![]() 、
、![]() ,若
,若![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=12,点D在边BC上,点E在线段AD上,EF⊥AC于点F,EG⊥EF交AB于点G,若EF=EG,则CD的长为( )
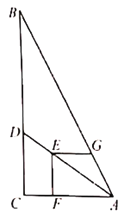
A.3.6B.4C.4.8D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】体育课时,王明、赵丽、高洁、李虎四位同学围成一圈玩传球游戏(假设传球的对象都是随机的),若开始时球在王明手中.
(1)经过一次传球后,球在高洁手里的概率是多少?
(2)求:经过两次传球后,球又回到王明手中的概率(用树状图或列表法求解)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com