
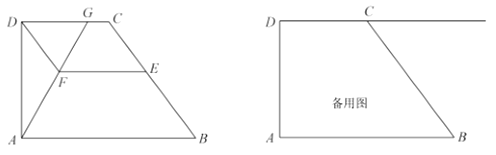
【题目】如图,已知梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 是边
是边![]() 上一点,过
上一点,过![]() 、
、![]() 分别作
分别作![]() 、
、![]() 的平行线交于点
的平行线交于点![]() ,联结
,联结![]() 并延长,与射线
并延长,与射线![]() 交于点
交于点![]() .
.
(1)当点![]() 与点
与点![]() 重合时,求
重合时,求![]() 的值;
的值;
(2)当点![]() 在边
在边![]() .上时,设
.上时,设![]() ,求
,求![]() 的面积;(用含
的面积;(用含![]() 的代数式表示)
的代数式表示)
(3)当![]() 时,求
时,求![]() 的余弦值.
的余弦值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)由题意可得四边形DCEF是平行四边形,可得CD=EF,通过证明△CFE∽△CAB进行分析求值即可;
(2)根据题意延长AG,BC交为于点M,过点C作CN⊥AB于点N,交EF于点H,由题意可得四边形ADCN是矩形,可得AD=CN=4,CD=AN=3,BN=3,由平行线分线段成比例可求BE,ME,MC,CH,GC的长,即可求GD的长,由三角求形面积公式可△DFG的面积;
(3)根据题意由△AFD∽△ADG,可得∠AFD=∠ADG=90°,由余角的性质可得∠DAG=∠B,即可求∠DAG的余弦值.
解:(1)如图,
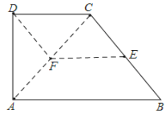
∵DC∥EF,DF∥CE,
∴四边形DCEF是平行四边形,
∴CD=EF,
∵AB=2CD=6,
∴AB=2EF,
∵EF∥CD,AB∥CD,
∴EF∥AB,
∴△CFE∽△CAB,
∴![]() ,
,
∴BC=2CE,
∴BE=CE,
∴EC:BE=1:1=1.
(2)如图,延长AG,BC交为于点M,过点C作CN⊥AB于点N,交EF于点H,
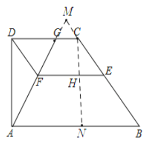
∵AD⊥CD,CN⊥CD,
∴AD∥CN,且CD∥AB,
∴四边形ADCN是平行四边形,
又∵∠DAB=90°,
∴四边形ADCN是矩形,
∴AD=CN=4,CD=AN=3,
∴BN=AB-AN=3,
在Rt△BCN中,BC=![]() ,
,
∴BE=BC-CE=5-m,
∵EF∥AB,
∴![]() 即
即![]() ,
,
∴ME=BE=5-m,
∴MC=ME-CE=5-2m,
∵EF∥AB,
∴![]() ,
,
∴HC=![]() ,
,
∵CG∥EF,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
(3)过点C作CN⊥AB于点N,
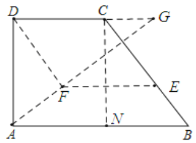
∵AB∥CD,∠DAB=90°,
∴∠DAB=∠ADG=90°,
若△AFD∽△ADG,
∴∠AFD=∠ADG=90°,
∴DF⊥AG,
又∵DF∥BC,
∴AG⊥BC,
∴∠B+∠GAB=90°,且∠DAG+∠GAB=90°,
∴∠B=∠DAG,
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,以
,以![]() 为直径作圆
为直径作圆![]() ,分别交
,分别交![]() 于点
于点![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() 交线段
交线段![]() 于点
于点![]() .
.
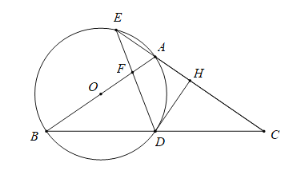
(1)求证:![]() 是圆
是圆![]() 的切线;
的切线;
(2)若![]() 为
为![]() 的中点,求
的中点,求![]() 的值;
的值;
(3)若![]() ,求圆
,求圆![]() 的半径.
的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场为了吸引顾客,设立了一个可以自由转动的转盘,如图所示,并规定:顾客消费200元(含200元)以上,就能获得一次转动转盘的机会,如果转盘停止后,指针正好对准九折、八折、七折区域,顾客就可以获得此项优惠,如果指针恰好在分割线上时,则需重新转动转盘.
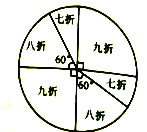
(1)某顾客正好消费220元,他转一次转盘,他获得九折、八折、七折优惠的概率分别是多少?
(2)某顾客消费中获得了转动一次转盘的机会,实际付费168元,请问他消费所购物品的原价应为多少元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校在宣传“民族团结”活动中,采用四种宣传形式:A.器乐,B.舞蹈,C.朗诵,D.唱歌.每名学生从中选择并且只能选择一种最喜欢的,学校就宣传形式对学生进行了抽样调查,并将调查结果绘制了如下两幅不完整的统计图.
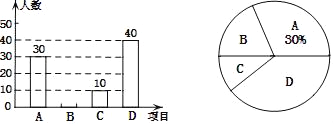
请结合图中所给信息,解答下列问题:
(1)本次调查的学生共有_____人;
(2)补全条形统计图;
(3)该校共有1200名学生,请估计选择“唱歌”的学生有多少人?
(4)七年一班在最喜欢“器乐”的学生中,有甲、乙、丙、丁四位同学表现优秀,现从这四位同学中随机选出两名同学参加学校的器乐队,请用列表或画树状图法求被选取的两人恰好是甲和乙的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
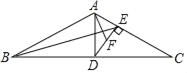
【题目】如图,在△ABC中,AB=AC,D是边BC的中点,DE⊥AC,垂足为点 E.
(1)求证:DECD=ADCE;
(2)设F为DE的中点,连接AF、BE,求证:AFBC=ADBE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若一个三角形一条边的平方等于另两条的乘积,我们把这个三角形叫做比例三角形.
(1)已知![]() 是比例三角形,
是比例三角形,![]() ,
,![]() ,请直接写出所有满足条件的
,请直接写出所有满足条件的![]() 的长;
的长;
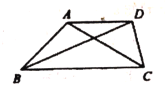
(2)如图,在四边形![]() 中,
中,![]() ,对角线
,对角线![]() 平分
平分![]() ,
,![]() .求证:
.求证:![]() 是比例三角形;
是比例三角形;
查看答案和解析>>
科目:初中数学 来源: 题型:
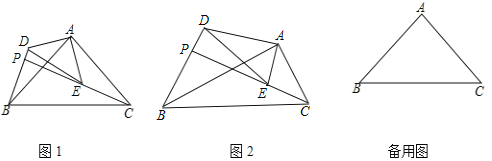
【题目】如图,![]() 和
和![]() 是有公共顶点的直角三角形,
是有公共顶点的直角三角形,![]() ,点P为射线BD,CE的交点.
,点P为射线BD,CE的交点.
(1)如图1,若![]() 和
和![]() 是等腰三角形,求证:
是等腰三角形,求证:![]() ;
;
(2)如图2,若![]() ,问:(1)中的结论是否成立?请说明理由.
,问:(1)中的结论是否成立?请说明理由.
(3)在(1)的条件下,若![]() ,
,![]() ,若把
,若把![]() 绕点A旋转,当
绕点A旋转,当![]() 时,求PB的长.
时,求PB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于一个函数,如果它的自变量 x 与函数值 y 满足:当1≤x≤1 时,1≤y≤1,则称这个函数为“闭 函数”.例如:y=x,y=x 均是“闭函数”. 已知 y ax2 bx c(a0) 是“闭函数”,且抛物线经过点 A(1,1)和点 B(1,1),则 a 的取值范围是______________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com