
科目: 来源:四川省达州市2018届中考二模试卷数学试卷 题型:填空题
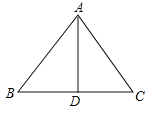
(2017黑龙江省齐齐哈尔市)如图,在等腰三角形纸片ABC中,AB=AC=10,BC=12,沿底边BC上的高AD剪成两个三角形,用这两个三角形拼成平行四边形,则这个平行四边形较长的对角线的长是______.
查看答案和解析>>
科目: 来源:四川省达州市2018届中考二模试卷数学试卷 题型:解答题
某中学为开拓学生视野,开展“课外读书周”活动,活动后期随机调查了九年级部分学生一周的课外阅读时间,并将结果绘制成两幅不完整的统计图,请你根据统计图的信息回答下列问题:

(1)本次调查的学生总数为_____人,被调查学生的课外阅读时间的中位数是_____小时,众数是_____小时;并补全条形统计图;
(2)在扇形统计图中,课外阅读时间为5小时的扇形的圆心角度数是_____;
(3)若全校九年级共有学生800人,估计九年级一周课外阅读时间为6小时的学生有多少人?
查看答案和解析>>
科目: 来源:四川省达州市2018届中考二模试卷数学试卷 题型:解答题
小方与同学一起去郊游,看到一棵大树斜靠在一小土坡上,他想知道树有多长,于是他借来测角仪和卷尺.如图,他在点C处测得树AB顶端A的仰角为30°,沿着CB方向向大树行进10米到达点D,测得树AB顶端A的仰角为45°,又测得树AB倾斜角∠1=75°.
(1)求AD的长.
(2)求树长AB.

查看答案和解析>>
科目: 来源:四川省达州市2018届中考二模试卷数学试卷 题型:解答题
旅游公司在景区内配置了50辆观光车共游客租赁使用,假定每辆观光车一天内最多只能出租一次,且每辆车的日租金x(元)是5的倍数.发现每天的营运规律如下:当x不超过100元时,观光车能全部租出;当x超过100元时,每辆车的日租金每增加5元,租出去的观光车就会减少1辆.已知所有观光车每天的管理费是1100元.
(1)优惠活动期间,为使观光车全部租出且每天的净收入为正,则每辆车的日租金至少应为多少元?(注:净收入=租车收入﹣管理费)
(2)当每辆车的日租金为多少元时,每天的净收入最多?
查看答案和解析>>
科目: 来源:四川省达州市2018届中考二模试卷数学试卷 题型:解答题
如图,在△ABC,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且∠CBF= ∠CAB.
∠CAB.
(1)求证:直线BF是⊙O的切线;
(2)若AB=5,sin∠CBF= ,求BC和BF的长.
,求BC和BF的长.

查看答案和解析>>
科目: 来源:四川省达州市2018届中考二模试卷数学试卷 题型:解答题
如图,一次函数y=kx+b的图象与反比例函数y= (x>0)的图象交于点P(n,2),与x轴交于点A(-4,0),与y轴交于点C,PB⊥x轴于点B,点A与点B关于y轴对称.
(x>0)的图象交于点P(n,2),与x轴交于点A(-4,0),与y轴交于点C,PB⊥x轴于点B,点A与点B关于y轴对称.
(1)求一次函数,反比例函数的表达式;
(2)求证:点C为线段AP的中点;
(3)反比例函数图象上是否存在点D,使四边形BCPD为菱形?如果存在,说明理由并求出点D的坐标;如果不存在,说明理由.

查看答案和解析>>
科目: 来源:四川省达州市2018届中考二模试卷数学试卷 题型:解答题
正方形ABCD的边长为3,点E,F分别在射线DC,DA上运动,且DE=DF.连接BF,作EH⊥BF所在直线于点H,连接CH.
(1)如图1,若点E是DC的中点,CH与AB之间的数量关系是 ;
(2)如图2,当点E在DC边上且不是DC的中点时,(1)中的结论是否成立?若成立给出证明;若不成立,说明理由;
(3)如图3,当点E,F分别在射线DC,DA上运动时,连接DH,过点D作直线DH的垂线,交直线BF于点K,连接CK,请直接写出线段CK长的最大值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com