
科目: 来源: 题型:
【题目】甲、乙两家超市同价销售同一款可拆分式驱蚊器,1套驱蚊器由1个加热器和1瓶电热蚊香液组成.电热蚊香液作为易耗品可单独购买,1瓶电热蚊香液的售价是1套驱蚊器的![]() .已知电热蚊香液的利润率为20%,整套驱蚊器的利润率为25%.张阿姨从甲超市买了1套这样的驱蚊器,并另外买了4瓶电热蚊香液,超市从中共获利10元.
.已知电热蚊香液的利润率为20%,整套驱蚊器的利润率为25%.张阿姨从甲超市买了1套这样的驱蚊器,并另外买了4瓶电热蚊香液,超市从中共获利10元.
(1)求1套驱蚊器和1瓶电热蚊香液的售价;
(2)为了促进该款驱蚊器的销售,甲超市打8.5折销售,而乙超市采用的销售方法是顾客每买1套驱蚊器送1瓶电热蚊香液.在这段促销期间,甲超市销售2000套驱蚊器,而乙超市在驱蚊器销售上获得的利润不低于甲超市的1.2倍.问乙超市至少销售多少套驱蚊器?
查看答案和解析>>
科目: 来源: 题型:
【题目】我们给出如下定义:顺次连接任意一个四边形各边中点所得的四边形叫中点四边形.

(1)如图1,四边形ABCD中,点E,F,G,H分别为边AB,BC,CD,DA的中点.求证:中点四边形EFGH是平行四边形;
(2)如图2,点P是四边形ABCD内一点,且满足PA=PB,PC=PD,∠APB=∠CPD,点E,F,G,H分别为边AB,BC,CD,DA的中点,猜想中点四边形EFGH的形状,并证明你的猜想;
(3)若改变(2)中的条件,使∠APB=∠CPD=90°,其他条件不变,直接写出中点四边形EFGH的形状.(不必证明)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,抛物线y=ax2﹣2ax+c(a≠0)与y轴交于点C(0,4),与x轴交于点A、B,点A坐标为(4,0).
(1)求该抛物线的解析式;
(2)抛物线的顶点为N,在x轴上找一点K,使CK+KN最小,并求出点K的坐标;
(3)点Q是线段AB上的动点,过点Q作QE∥AC,交BC于点E,连接CQ.当△CQE的面积最大时,求点Q的坐标;
(4)若平行于x轴的动直线l与该抛物线交于点P,与直线AC交于点F,点D的坐标为(2,0).问:是否存在这样的直线l,使得△ODF是等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】在△ABC中,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B、C重合),以AD为边在AD的右侧作正方形ADEF,连接CF.
(1)观察猜想:如图(1),当点D在线段BC上时,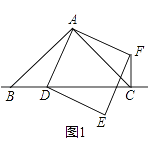
①BC与CF的位置关系是:;
②BC、CD、CF之间的数量关系为:(将结论直接写在横线上)
(2)数学思考:如图(2),当点D在线段CB的延长线上时,上述①、②中的结论是否仍然成立?若成立,请给予证明,若不成立,请你写出正确结论再给予证明.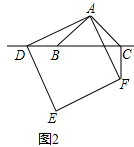
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,O是AB边上的一点,以OA为半径的⊙O与边BC相切于点E. 
(1)若AC=6,BC=10,求⊙O的半径.
(2)过点E作弦EF⊥AB于M,连接AF,若∠AFE=2∠ABC,求证:四边形ACEF是菱形.
查看答案和解析>>
科目: 来源: 题型:
【题目】在下列解题过程的空白处填上适当的内容(推理的理由或数学表达式)
如图,在△ABC中,已知∠ADE=∠B,∠1=∠2,FG⊥AB于点G.

求证CD⊥AB.
证明:∵∠ADE=∠B(已知),
∴ ( ),
∵ DE∥BC(已证),
∴ ( ),
又∵∠1=∠2(已知),
∴ ( ),
∴CD∥FG( ),
∴ (两直线平行同位角相等),
∵ FG⊥AB(已知),
∴∠FGB=90°(垂直的定义).
即∠CDB=∠FGB=90°,
∴CD⊥AB. (垂直的定义).
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系中,一次函数y=ax+b(a≠0)的图形与反比例函数y= ![]() (k≠0)的图象交于第二、四象限内的A、B两点,与y轴交于C点,过点A作AH⊥y轴,垂足为H,OH=3,tan∠AOH=
(k≠0)的图象交于第二、四象限内的A、B两点,与y轴交于C点,过点A作AH⊥y轴,垂足为H,OH=3,tan∠AOH= ![]() ,点B的坐标为(m,﹣2).
,点B的坐标为(m,﹣2). 
(1)求△AHO的周长;
(2)求该反比例函数和一次函数的解析式.
查看答案和解析>>
科目: 来源: 题型:
【题目】画图并填空:如图,方格纸中每个小正方形的边长都为1.在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点D的对应点D′.
(1)根据特征画出平移后的△A′B′C′;
(2)利用网格的特征,画出AC边上的高BE并标出画法过程中的特征点;
(3)△A′B′C′的面积为 .

查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,回答下列问题:
(1)比较∠FOD与∠FOE的大小;
(2)借助三角板比较∠DOE与∠BOF的大小;
(3)借助量角器比较∠AOE与∠DOF的大小.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com