A. 商贩A的单价大于商贩B的单价

B. 商贩A的单价等于商贩B的单价

C. 商版A的单价小于商贩B的单价

D. 赔钱与商贩A、商贩B的单价无关

【题目】“保护好环境，拒绝冒黑烟”．某市公交公司将淘汰某一条线路上“冒黑烟”较严重的公交车，计划购买A型和B型两种环保节能公交车共10辆，若购买A型公交车1辆，B型公交车2辆，共需400万元；若购买A型公交车2辆，B型公交车1辆，共需350万元．
（1）求购买A型和B型公交车每辆各需多少万元？
（2）预计在该线路上A型和B型公交车每辆年均载客量分别为60万人次和100万人次．若该公司购买A型和B型公交车的总费用不超过1200万元，且确保这10辆公交车在该线路的年均载客总和不少于680万人次，则该公司有哪几种购车方案？哪种购车方案总费用最少？最少总费用是多少？

（1）下列选取样本的方法最合理的一种是 ．（只需填上正确答案的序号）

①在市中心某个居民区以家庭为单位随机抽取；②在全市医务工作者中以家庭为单位随机抽取；③在全市常住人口中以家庭为单位随机抽取．

（2）本次抽样调査发现，接受调査的家庭都有过期药品，现将有关数据呈现如图：

①m= ，n= ；

②补全条形统计图；

③根据调査数据，你认为该市市民家庭处理过期药品最常见的方式是什么？

④家庭过期药品的正确处理方式是送回收点，若该市有180万户家庭，请估计大约有多少户家庭处理过期药品的方式是送回收点．

（1）设一个月内在本地通话时间为分钟，全球通收费表示为 元，神州行收费表示为 元

（2）若某用户一个月内本地通话时间为2.5小时，你认为选择哪种方式较为划算？

（3）当通话时间为多少时间，两种收费方式的费用是一样的？

【题目】如图1，四边形ABCD是正方形，点E是边BC上一点，点F在射线CM上，∠AEF=90°，AE=EF，过点F作射线BC的垂线，垂足为H，连接AC．
（1）试判断BE与FH的数量关系，并说明理由；
（2）求证：∠ACF=90°；
（3）连接AF，过A、E、F三点作圆，如图2，若EC=4，∠CEF=15°，求 的长．

某校七年级（1）、（2）两个班104人去游园，其中七（1）班不足50人，（2）班超过50人，但不足100人。经估算，如果两个班都以班为单位购票，则一共应付1240元。问：

（1）两班各有多少学生？

（2）如果两班联合起来，作为一个团体购票，可省多少钱？

（3）如果七（1）班单独组织去游园，作为组织者的你将如何购票才最省钱？

【题目】某地居民生活用电基本价格为每度电0.4元，若每月用电量不超过度时，按基本价格收费；若超过度，超出部分按基本价格的150%收费.

（1）某户8月份用电84度，共交电费38.4元，求的值。

（2）如果该户9月份的电费平均为每度0.5元，那么该用户9月份用电多少度？应交电费多少元？

【题目】在平面直角坐标系中，抛物线y=x2+（k﹣1）x﹣k与直线y=kx+1交于A，B两点，点A在点B的左侧．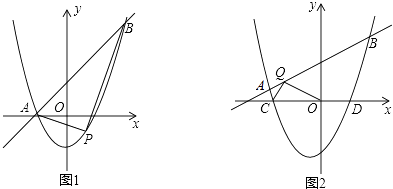

（1）如图1，当k=1时，直接写出A，B两点的坐标；
（2）在（1）的条件下，点P为抛物线上的一个动点，且在直线AB下方，试求出△ABP面积的最大值及此时点P的坐标；
（3）如图2，抛物线y=x2+（k﹣1）x﹣k（k＞0）与x轴交于点C、D两点（点C在点D的左侧），在直线y=kx+1上是否存在唯一一点Q，使得∠OQC=90°？若存在，请求出此时k的值；若不存在，请说明理由．

【题目】已知，抛物线y=ax2+bx+c（a≠0）经过原点，顶点为A（h，k）（h≠0）．
（1）当h=1，k=2时，求抛物线的解析式；
（2）若抛物线y=tx2（t≠0）也经过A点，求a与t之间的关系式；
（3）当点A在抛物线y=x2﹣x上，且﹣2≤h＜1时，求a的取值范围．

【题目】如图，矩形ABCD中，AB=4，AD=3，M是边CD上一点，将△ADM沿直线AM对折，得到△ANM．

（1）当AN平分∠MAB时，求DM的长；
（2）连接BN，当DM=1时，求△ABN的面积；
（3）当射线BN交线段CD于点F时，求DF的最大值．