
科目: 来源: 题型:
【题目】如图,在△ABC中,∠A=45°,∠B=60°,AB=4,P是BC边上的动点(不与B,C重合),点P关于直线AB,AC的对称点分别为M,N,则线段MN长的取值范围是 . 
查看答案和解析>>
科目: 来源: 题型:
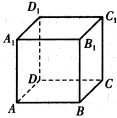
【题目】如图,设正方体ABCD-A1B1C1D1的棱长为1,黑、白两个甲壳虫同时从点A出发,以相同的速度分别沿棱向前爬行,黑甲壳虫爬行的路线是AA1→A1D1→…,白甲壳虫爬行的路线是AB→BB1→…,并且都遵循如下规则:所爬行的第n+2与第n条棱所在的直线必须是既不平行也不相交(其中n是正整数),那么当黑、白两个甲壳虫各爬行完第2013条棱分别停止在所到的正方体顶点处时,它们之间的距离是 .
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,正六边形ABCDEF的边长为6cm,P是对角线BE上一动点,过点P作直线l与BE垂直,动点P从B点出发且以1cm/s的速度匀速平移至E点.设直线l扫过正六边形ABCDEF区域的面积为S(cm2),点P的运动时间为t(s),下列能反映S与t之间函数关系的大致图象是( )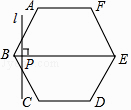
A.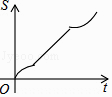
B.
C.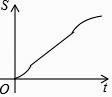
D.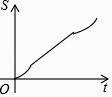
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知直线y= ![]() x﹣2与x轴交于点A,与y轴交于点C,经过A、C两点的抛物线与轴交于另一点B(1,0).
x﹣2与x轴交于点A,与y轴交于点C,经过A、C两点的抛物线与轴交于另一点B(1,0).
(1)求该抛物线的解析式.
(2)在直线y= ![]() x﹣2上方的抛物线上存在一动点D,连接AD、CD,设点D的横坐标为m,△DCA的面积为S,求S与m的函数关系式,并求出S的最大值.
x﹣2上方的抛物线上存在一动点D,连接AD、CD,设点D的横坐标为m,△DCA的面积为S,求S与m的函数关系式,并求出S的最大值.
(3)在抛物线上是否存在一点M,使得以M为圆心,以 ![]() 为半径的圆与直线AC相切?若存在,请求出点M的坐标;若不存在,请说明理由.
为半径的圆与直线AC相切?若存在,请求出点M的坐标;若不存在,请说明理由.
(4)在y轴的正半轴上存在一点P,使∠APB的值最大,请直接写出当∠APB最大时点P的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知线段MN=8,C是线段MN上一动点,在MN的同侧分别作等边△CMD和等边△CNE.
(1)如图①,连接DN与EM,两条线段相交于点H,求证ME=DN,并求∠DHM的度数;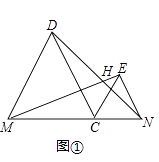
(2)如图②,过点D、E分别作线段MN的垂线,垂足分别为F、G,问:在点C运动过程中,DF+EG的长度是否为定值,如果是,请求出这个定值,如果不是请说明理由;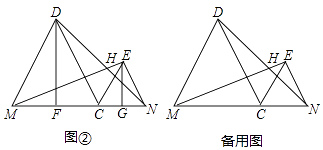
(3)当点C由点M移到点N时,点H移到的路径长度为(直接写出结果)
查看答案和解析>>
科目: 来源: 题型:
【题目】某校九年级(1)班准备购买大课间活动器材呼啦圈和跳绳,已知购买1根跳绳和2个呼啦圈要35元,购买2根跳绳和1个呼啦圈要25元.
(1)求每根跳绳、每个呼啦圈各多少元?
(2)根据班级实际情况,需购买跳绳和呼啦圈的总数量为30,总费用不超过300元,但不低于280元,请你通过计算求出有几种购买方案,哪种方案费用最低.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,在矩形纸片ABCD中,AB=3cm,AD=5cm,折叠纸片使B点落在边AD上的E处,折痕为PQ,过点E作EF∥AB交PQ于F,连接BF.
(1)求证:四边形BFEP为菱形;
(2)当点E在AD边上移动时,折痕的端点P、Q也随之移动;
①当点Q与点C重合时(如图2),求菱形BFEP的边长;
②若限定P、Q分别在边BA、BC上移动,求出点E在边AD上移动的最大距离.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,点D在⊙O的直径AB的延长线上,点C在⊙O上,AC=CD,∠ACD=120°. 
(1)求证:CD是⊙O的切线;
(2)若⊙O的半径为4,求图中阴影部分的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,小华在A处利用高为1.5米的测角仪AB测得楼EF顶部E的仰角为30°,然后前进30米到达C处,又测得顶部E的仰角为60°,求大楼EF的高度.(结果精确到0.1米,参考数据 ![]() =1.732)
=1.732)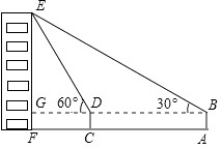
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com