
科目: 来源: 题型:
【题目】如图所示,已知AB是圆O的直径,圆O过BC的中点D,且DE⊥AC. 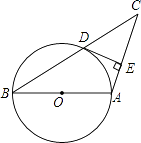
(1)求证:DE是圆O的切线;
(2)若∠C=30°,CD=10cm,求圆O的半径.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,四边形OABC四个顶点的坐标分别为O(0,0),A(﹣3,0),B(﹣4,2),C(﹣1,2).将四边形OABC绕点O顺时针旋转90°后,点A,B,C分别落在点A′,B′,C′处. 
(1)请你在所给的直角坐标系中画出旋转后的四边形OA′B′C′;
(2)点C旋转到点C′所经过的弧的半径是 , 点C经过的路线长是 .
查看答案和解析>>
科目: 来源: 题型:
【题目】根据题意,列方程
(1)某数与8的和的2倍比它自己大11,求这个数.
(2)某老师准备在期末对学生进行奖励,到文具店买了20本练习簿和30支铅笔,共花了16元,现在知道练习簿比铅笔贵3角.求练习簿和铅笔单价?
(3)某产品的成本价为25元,现在按标价的8折销售,还可以有10元的利润,求此产品的标价?
(4)某文件需要打印,小李独立做需要6小时完成,小王独立做需要9小时完成.现在他们俩共同做了3小时,剩下的工作由小王独自做完.问小王还要用多少小时把剩下的工作做完?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,直线y=k1x(x≥0)与双曲线y=![]() (x>0)相交于点P(2,4).已知点A(4,0),B(0,3),连接AB,将Rt△AOB沿OP方向平移,使点O移动到点P,得到△A′PB′.过点A′作A′C∥y轴交双曲线于点C,连接CP.
(x>0)相交于点P(2,4).已知点A(4,0),B(0,3),连接AB,将Rt△AOB沿OP方向平移,使点O移动到点P,得到△A′PB′.过点A′作A′C∥y轴交双曲线于点C,连接CP.
(1)求k1与k2的值;
(2)求直线PC的解析式;
(3)直接写出线段AB扫过的面积.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=mx+n(m≠0)的图象与反比例函数y=![]() (k≠0)的图象交于第一、三象限内的A、B两点,与y轴交于点C,过点B作BM⊥x轴,垂足为M,BM=OM,OB=2
(k≠0)的图象交于第一、三象限内的A、B两点,与y轴交于点C,过点B作BM⊥x轴,垂足为M,BM=OM,OB=2![]() ,点A的纵坐标为4.
,点A的纵坐标为4.
(1)求该反比例函数和一次函数的解析式;
(2)连接MC,求四边形MBOC的面积.

查看答案和解析>>
科目: 来源: 题型:
【题目】已知二次函数的解析式是y=x2﹣2x﹣3
(1)用配方法将y=x2﹣2x﹣3化成y=a(x﹣h)2+k的形式;
(2)在直角坐标系中,用五点法画出它的图像; 
(3)利用图象求当x为何值时,函数值y<0
(4)当x为何值时,y随x的增大而减小?
(5)当﹣3<x<3时,观察图象直接写出函数值y的取值的范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】下列变形中:
①由方程![]() =2去分母,得x﹣12=10;
=2去分母,得x﹣12=10;
②由方程![]() x=
x=![]() 两边同除以
两边同除以![]() ,得x=1;
,得x=1;
③由方程6x﹣4=x+4移项,得7x=0;
④由方程2﹣![]() 两边同乘以6,得12﹣x﹣5=3(x+3).
两边同乘以6,得12﹣x﹣5=3(x+3).
错误变形的个数是( )个.
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,直线AB与函数y=![]() (x>0)的图象交于点A(m,2),B(2,n).过点A作AC平行于x轴交y轴于点C,在y轴负半轴上取一点D,使OD=
(x>0)的图象交于点A(m,2),B(2,n).过点A作AC平行于x轴交y轴于点C,在y轴负半轴上取一点D,使OD=![]() OC,且△ACD的面积是6,连接BC.
OC,且△ACD的面积是6,连接BC.
(1)求m,k,n的值;
(2)求△ABC的面积.

查看答案和解析>>
科目: 来源: 题型:
【题目】自2014年12月28日北京公交地铁调价以来,人们的出行成本发生了较大的变化. 小林根据新闻,将地铁和公交车的票价绘制成了如下两个表格。(说明:表格中“6~12公里”指的是大于6公里,小于等于12公里,其他类似)
|
| ||||||||||||||||||||||||||||||
根据以上信息回答下列问题:
小林办了一张市政交通一卡通学生卡,目前乘坐地铁没有折扣。
(1)如果小林全程乘坐地铁的里程为14公里,用他的学生卡需要刷卡交费________元;
(2)如果小林全程乘坐公交车的里程为16公里,用他的学生卡需要刷卡交________元;
(3)小林用他的学生卡乘坐一段地铁后换乘公交车,两者累计里程为12公里。已知他乘坐地铁平均每公里花费0.4元,乘坐公交车平均每公里花费0.25元,此次行程共花费4.5元。请问小林乘坐地铁和公交车的里程分别是多少公里?
查看答案和解析>>
科目: 来源: 题型:
【题目】程大位所著《算法统宗》是一部中国传统数学重要的著作.在《算法统宗》中记载:“平地秋千未起,踏板离地一尺.送行二步与人齐,五尺人高曾记.仕女佳人争蹴,终朝笑语欢嬉.良工高士素好奇,算出索长有几?”【注释】1步=5尺.
译文:“当秋千静止时,秋千上的踏板离地有1尺高,如将秋千的踏板往前推动两步(10尺)时,踏板就和人一样高,已知这个人身高是5尺.美丽的姑娘和才子们,每天都来争荡秋千,欢声笑语终日不断.好奇的能工巧匠,能算出这秋千的绳索长是多少吗?”
如图,假设秋千的绳索长始终保持直线状态,OA是秋千的静止状态,A是踏板,CD是地面,点B是推动两步后踏板的位置,弧AB是踏板移动的轨迹.已知AC=1尺,CD=EB=10尺,人的身高BD=5尺.设绳索长OA=OB=x尺,则可列方程为 . 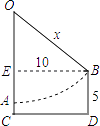
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com