用于购买奖品的总费用不少于1000元但不超过1100元，小明在购买“福娃”和微章前，了解到如下信息：

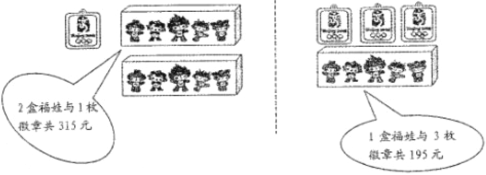
（1）求一盒“福娃”和一枚徽章各多少元？

（2）若本次活动设一等奖2名，则二等奖和三等奖应各设多少名？

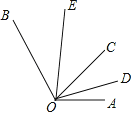
A. ∠DOE的度数不能确定 B. ∠AOD=∠EOC

C. ∠AOD+∠BOE=65° D. ∠BOE=2∠COD

政府相关部门批给该村沼气池修建用地708平方米．设修建A型沼气池x个，修建两种型号沼气池共需费用y万元．

（1）用含有x的代数式表示y；

（2）不超过政府批给修建沼气池用地面积，又要使该村每户村民用上沼气的修建方案有几种；

（3）若平均每户村民集资700元，能否满足所需费用最少的修建方案．

【题目】如图，已知抛物线与x轴交于A（﹣1，0）、B（5，0）两点，与y轴交于点C（0，5）．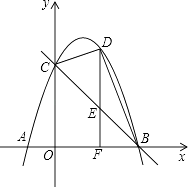

（1）求该抛物线所对应的函数关系式；
（2）D是笫一象限内抛物线上的一个动点（与点C、B不重合），过点D作DF⊥x轴于点F，交直线BC于点E，连结BD、CD．设点D的横坐标为m，△BCD的面积为S．
①求S关于m的函数关系式及自变量m的取值范围；
②当m为何值时，S有最大值，并求这个最大值；
③直线BC能否把△BDF分成面积之比为2：3的两部分？若能，请求出点D的坐标；若不能，请说明理由．

【题目】已知△ABC是等腰直角三角形，∠BAC=90°，CD= BC，DE⊥CE，DE=CE，连接AE，点M是AE的中点．
（1）如图1，若点D在BC边上，连接CM，当AB=4时，求CM的长；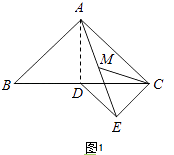
（2）如图2，若点D在△ABC的内部，连接BD，点N是BD中点，连接MN，NE，求证：MN⊥AE；
（3）如图3，将图2中的△CDE绕点C逆时针旋转，使∠BCD=30°，连接BD，点N是BD中点，连接MN，探索 的值并直接写出结果．

（1）设运送这批货物的总费用为y万元，这列货车挂A型车厢x 节，试定出用车厢节数x表示总费用y的公式.

（2）如果每节A型车厢最多可装甲种货物35吨和乙种货物15吨，每节B型车厢最多可装甲种货物25吨和乙种货物35吨，装货时按此要求安排A、B两种车厢的节数，那么共有哪几种安排车厢的方案？

(1)若直线CD经过∠BCA的内部，且E，F在射线CD上，请解决下面两个问题：

①如图(a)，若∠BCA＝90°，α＝90°，则BE________CF，EF________|BE－AF|(填“>”“<”或“＝”)；

②如图(b)，若0°＜∠BCA＜180°，请添加一个关于α与∠BCA关系的条件________，使①中的两个结论仍然成立，并证明两个结论成立；

(2)如图(c)，若直线CD经过∠BCA的外部，∠BCA＝α，请写出EF，BE，AF三条线段数量关系的合理猜想(不要求证明)．

(1)计算B的表达式；

(2)求出2A﹣B的结果；

(3)小强同学说(2)中的结果的大小与c的取值无关，对吗？若a=，b=，

求(2)中式子的值．

【题目】如图，AB∥CD，以点A为圆心，小于AC长为半径作圆弧，分别交AB，AC于E，F两点，再分别以E，F为圆心，大于EF长为半径作圆弧，两条圆弧交于点P，作射线AP，交CD于点M。

（1）若∠ACD=114°，求∠MAB的度数；

（2）若CN⊥AM，垂足为N，求证：△ACN≌△MCN。

【题目】如图，AC是⊙O的直径，BC是⊙O的弦，点P是⊙O外一点，连接PB、AB，∠PBA=∠C．
（1）求证：PB是⊙O的切线；
（2）连接OP，若OP∥BC，且OP=8，⊙O的半径为2 ，求BC的长．