
科目: 来源: 题型:
【题目】如图,在矩形ABCD中,AB=4,BC=6,点E为BC的中点,将△ABE沿AE折叠,使点B落在矩形内点F处,连接CF,则CF的长为( ) 
A.1.8
B.2.4
C.3.2
D.3.6
查看答案和解析>>
科目: 来源: 题型:
【题目】如图![]() ,在矩形
,在矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 从
从![]() 点出发,沿
点出发,沿![]() 路线运动,到
路线运动,到![]() 点停止;点
点停止;点![]() 从
从![]() 点出发,沿
点出发,沿![]() 运动,到
运动,到![]() 点停止.若点
点停止.若点![]() 、点
、点![]() 同时出发,点
同时出发,点![]() 的速度为每秒
的速度为每秒![]() ,点
,点![]() 的速度为每秒
的速度为每秒![]() ,
,![]() 秒时点
秒时点![]() 、点
、点![]() 同时改变速度,点
同时改变速度,点![]() 的速度变为每秒
的速度变为每秒![]() ,点
,点![]() 的速度变为每秒
的速度变为每秒![]() .如图
.如图![]() 是点
是点![]() 出发
出发![]() 秒后
秒后![]() 的面积
的面积![]() 与
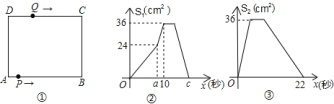
与![]() (秒)的函数关系图象;图
(秒)的函数关系图象;图![]() 是点
是点![]() 出发
出发![]() 秒后
秒后![]() 的面积
的面积![]() 与
与![]() (秒)的函数关系图象.根据图象:
(秒)的函数关系图象.根据图象:
![]() 求
求![]() 、
、![]() 、
、![]() 的值;
的值;
![]() 设点
设点![]() 出发
出发![]() (秒)后离开点
(秒)后离开点![]() 的路程为
的路程为![]() ,请写出
,请写出![]() 与
与![]() 的函数关系式,并求出点
的函数关系式,并求出点![]() 与
与![]() 相遇时
相遇时![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,已知二次函数y=x2+bx+c的图象与x 轴交于A(﹣1,0)、B(3,0)两点,与y 轴交于点C,顶点为D,对称轴为直线l.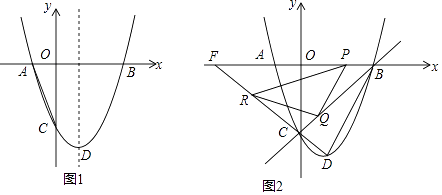
(1)求该二次函数的表达式;
(2)若点E 是对称轴l 右侧抛物线上一点,且S△ADE=2S△AOC , 求点E 的坐标;
(3)如图2,连接DC 并延长交x 轴于点F,设P 为线段BF 上一动点(不与B、F 重合),过点P 作PQ∥BD 交直线BC 于点Q,将直线PQ 绕点P 沿顺时针方向旋转45°后,所得的直线交DF 于点R,连接QR.请直接写出当△PQR 与△PFR 相似时点P 的坐标.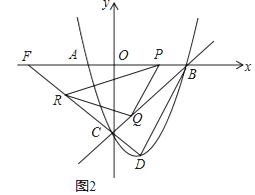
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系内,已知直线l1经过原点O 及A(2,2 ![]() )两点,将直线l1向右平移4个单位后得到直线l2 , 直线l2与x 轴交于点B.
)两点,将直线l1向右平移4个单位后得到直线l2 , 直线l2与x 轴交于点B. 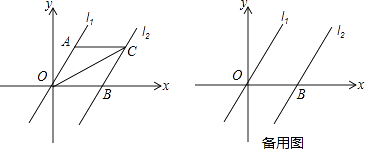
(1)求直线l2的函数表达式;
(2)作∠AOB 的平分线交直线l2于点C,连接AC.求证:四边形OACB是菱形;
(3)设点P 是直线l2上一点,以P 为圆心,PB 为半径作⊙P,当⊙P 与直线l1相切时,请求出圆心P 点的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】某电器商场销售甲、乙两种品牌空调,已知每台乙种品牌空调的进价比每台甲种品牌空调的进价高20%,用7200元购进的乙种品牌空调数量比用3000元购进的甲种品牌空调数量多2 台.
(1)求甲、乙两种品牌空调的进货价;
(2)该商场拟用不超过16000 元购进甲、乙两种品牌空调共10台进行销售,其中甲种品牌空调的售价为2500元/台,乙种品牌空调的售价为3500元/台.请你帮该商场设计一种进货方案,使得在售完这10 台空调后获利最大,并求出最大利润.
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读下列材料:
关于x的方程:![]() 的解是
的解是![]() ,
,![]() ;
;![]() 即
即![]() 的解是
的解是![]() ;
;![]() 的解是
的解是![]() ,
,![]() ;
;![]() 的解是
的解是![]() ,
,![]() ;
;![]()
![]() 请观察上述方程与解的特征,比较关于x的方程
请观察上述方程与解的特征,比较关于x的方程![]() 与它们的关系,猜想它的解是什么?并利用“方程的解”的概念进行验证.
与它们的关系,猜想它的解是什么?并利用“方程的解”的概念进行验证.
![]() 由上述的观察、比较、猜想、验证,可以得出结论:
由上述的观察、比较、猜想、验证,可以得出结论:
如果方程的左边是未知数与其倒数的倍数的和,方程的右边的形式与左边完全相同,只是把其中的未知数换成了某个常数,那么这样的方程可以直接得解,请用这个结论解关于x的方程:![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知矩形ABCD 中,E、F 分别为BC、AD 上的点,将四边形ABEF 沿直线EF 折叠后,点B 落在CD 边上的点G 处,点A 的对应点为点H.再将折叠后的图形展开,连接BF、GF、BG,若BF⊥GF. 
(1)求证:△ABF≌△DFG;
(2)已知AB=3,AD=5,求tan∠CBG 的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】现在,共享单车已遍布深圳街头,其中较为常见的共享单车有“A.摩拜单车”、“B.小蓝单车”、“C.OFO单车”、“D.小鸣单车”、“E.凡骑绿畅”等五种类型.为了解市民使用这些共享单车的情况,某数学兴趣小组随机统计部分正在使用这些单车的市民,并将所得数据绘制出了如下两幅不完整的统计图表 (图1、图2):
根据所给信息解答下列问题:
(1)此次统计的人数为人;根据已知信息补全条形统计图;
(2)在使用单车的类型扇形统计图中,使用E 型共享单车所在的扇形的圆心角为度;
(3)据报道,深圳每天有约200余万人次使用共享单车,则其中使用E型共享单车的约有万人次.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com