
科目: 来源: 题型:
【题目】已知梯形ABCD,AD∥BC,AB⊥BC,AD=1,AB=2,BC=3, 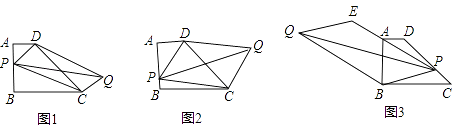
问题1:如图1,P为AB边上的一点,以PD,PC为边作平行四边形PCQD,请问对角线PQ,DC的长能否相等,为什么?
问题2:如图2,若P为AB边上一点,以PD,PC为边作平行四边形PCQD,请问对角线PQ的长是否存在最小值?如果存在,请求出最小值,如果不存在,请说明理由.
问题3:若P为AB边上任意一点,延长PD到E,使DE=PD,再以PE,PC为边作平行四边形PCQE,请探究对角线PQ的长是否也存在最小值?如果存在,请求出最小值,如果不存在,请说明理由.
问题4:如图3,若P为DC边上任意一点,延长PA到E,使AE=nPA(n为常数),以PE、PB为边作平行四边形PBQE,请探究对角线PQ的长是否也存在最小值?如果存在,请求出最小值,如果不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,甲、乙两人分别从A(1, ![]() )、B(6,0)两点同时出发,点O为坐标原点,甲沿AO方向、乙沿BO方向均以4km/h的速度行驶,th后,甲到达M点,乙到达N点.
)、B(6,0)两点同时出发,点O为坐标原点,甲沿AO方向、乙沿BO方向均以4km/h的速度行驶,th后,甲到达M点,乙到达N点. 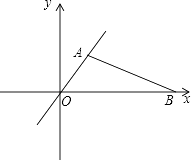
(1)请说明甲、乙两人到达O点前,MN与AB不可能平行;
(2)当t为何值时,△OMN∽△OBA;
(3)甲、乙两人之间的距离为MN的长,设s=MN2 , 求s与t之间的函数关系式,并求甲、乙两人之间距离的最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,抛物线y=﹣x2+bx+c与x轴交于A、B两点,与y轴交于点C,点O为坐标原点,点D为抛物线的顶点,点E在抛物线上,点F在x轴上,四边形OCEF为矩形,且OF=2,EF=3,
(1)求抛物线所对应的函数解析式;
(2)求△ABD的面积;
(3)将△AOC绕点C逆时针旋转90°,点A对应点为点G,问点G是否在该抛物线上?请说明理由.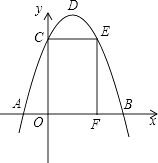
查看答案和解析>>
科目: 来源: 题型:
【题目】已知B港口位于A观测点北偏东53.2°方向,且其到A观测点正北方向的距离BD的长为16km,一艘货轮从B港口以40km/h的速度沿如图所示的BC方向航行,15min后达到C处,现测得C处位于A观测点北偏东79.8°方向,求此时货轮与A观测点之间的距离AC的长(精确到0.1km).(参考数据:sin53.2°≈0.80,cos53.2°≈0.60,sin79.8°≈0.98,cos79.8°≈0.18,tan26.6°≈0.50, ![]() ≈1.41,
≈1.41, ![]() ≈2.24)
≈2.24)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,⊙O的圆心在坐标原点,半径为2,直线y=x+b(b>0)与⊙O交于A、B两点,点O关于直线y=x+b的对称点O′. 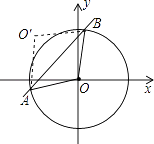
(1)求证:四边形OAO′B是菱形;
(2)当点O′落在⊙O上时,求b的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】现有5根小木棒,长度分别为:2、3、4、5、7(单位:cm),从中任意取出3根,
(1)列出所选的3根小木棒的所有可能情况;
(2)如果用这3根小木棒首尾顺次相接,求它们能搭成三角形的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】今年我市体育中考的现场选测项目中有一项是“排球30秒对墙垫球”,为了了解某学校九年级学生此项目平时的训练情况,随机抽取了该校部分九年级学生进行测试,根据测试结果,制作了如下尚不完整的频数分布表:
组别 | 垫球个数x(个) | 频数(人数) | 频率 |
1 | 10≤x<20 | 5 | 0.10 |
2 | 20≤x<30 | a | 0.18 |
3 | 30≤x<40 | 20 | b |
4 | 40≤x<50 | 16 | 0.32 |
合计 | 1 |
(1)表中a= , b=;
(2)这个样本数据的中位数在第组;
(3)下表为≤体育与健康≥中考察“排球30秒对墙垫球”的中考评分标准,若该校九年级有500名学生,请你估计该校九年级学生在这一项目中得分在7分以上(包括7分)学生约有多少人? 排球30秒对墙垫球的中考评分标准
分值 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
排球(个) | 40 | 36 | 33 | 30 | 27 | 23 | 19 | 15 | 11 | 7 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com