
【题目】解下列方程:
(1)4x+7=12x﹣5 (2)4y﹣3(5﹣y)=6;
(3)![]() (4)
(4)![]() =1.
=1.
【答案】(1) x=![]() ;(2) y=3;(3)x=﹣1;(4)a=4.4.
;(2) y=3;(3)x=﹣1;(4)a=4.4.
【解析】
(1)(2)移项再合并同类项即可解答.
(3)(4)先去分母,去括号,再移项合并同类项即可解答.
解:(1)移项,得:4x﹣12x=﹣5﹣7,
合并同类项,得:﹣8x=﹣12,
系数化为1,得:x=![]() ;
;
(2)去括号,得:4y﹣15+3y=6,
移项,得:4y+3y=6+15,
合并同类项,得:7y=21,
系数化为1,得:y=3;
(3)去分母,得:3(3x﹣1)﹣2(5x﹣7)=12,
去括号,得:9x﹣3﹣10x+14=12,
移项,得:9x﹣10x=12+3﹣14,
合并同类项,得:﹣x=1,
系数化为1,得:x=﹣1;
(4)整理,得:![]() ﹣
﹣![]() =1,
=1,
去分母,得:3(20a﹣3)﹣5(10a+4)=15,
去括号,得:60a﹣9﹣50a﹣20=15,
移项,得:60a﹣50a=15+9+20,
合并同类项,得:10a=44,
系数化为1,得:a=4.4.


 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:初中数学 来源: 题型:
【题目】轮船沿江从A港顺流行驶到B港,比从B港返回A港少用2小时,若船速为26千米/时,水速为3千米/时,求A港和B港相距多少千米.设A港和B港相距x千米.根据题意,可列出的方程是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某测量船位于海岛P的北偏西60°方向,距离海岛100海里的A处,它沿正南方向航行一段时间后,到达位于海岛P的西南方向上的B处,求测量船从A处航行到B处的路程(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某玩具由一个圆形区域和一个扇形区域组成,如图,在⊙O1和扇形O2CD中,⊙O1与O2C、O2D分别切于点A、B,已知∠CO2D=60°,E、F是直线O1O2与⊙O1、扇形O2CD的两个交点,且EF=24cm,设⊙O1的半径为xcm. 
(1)用含x的代数式表示扇形O2CD的半径;
(2)若⊙O1和扇形O2CD两个区域的制作成本分别为0.45元/cm2和0.06元/cm2 , 当⊙O1的半径为多少时,该玩具的制作成本最小?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年我市体育中考的现场选测项目中有一项是“排球30秒对墙垫球”,为了了解某学校九年级学生此项目平时的训练情况,随机抽取了该校部分九年级学生进行测试,根据测试结果,制作了如下尚不完整的频数分布表:
组别 | 垫球个数x(个) | 频数(人数) | 频率 |
1 | 10≤x<20 | 5 | 0.10 |
2 | 20≤x<30 | a | 0.18 |
3 | 30≤x<40 | 20 | b |
4 | 40≤x<50 | 16 | 0.32 |
合计 | 1 |
(1)表中a= , b=;
(2)这个样本数据的中位数在第组;
(3)下表为≤体育与健康≥中考察“排球30秒对墙垫球”的中考评分标准,若该校九年级有500名学生,请你估计该校九年级学生在这一项目中得分在7分以上(包括7分)学生约有多少人? 排球30秒对墙垫球的中考评分标准
分值 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
排球(个) | 40 | 36 | 33 | 30 | 27 | 23 | 19 | 15 | 11 | 7 |
查看答案和解析>>
科目:初中数学 来源: 题型:
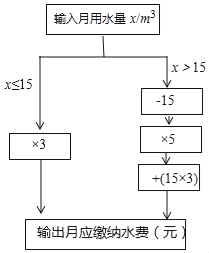
【题目】小明根据市自来水公司的居民用水收费标准,制定了水费计算数值转换机的示意图.(用水量单位:m3,水费单位:元)
(1)根据转换机程序计算下列各户月应缴纳水费
用户 | 张大爷 | 王阿姨 | 小明家 |
月用水量/m3 | 6 | 15 | 17 |
月应缴纳水费/元 |
|
|
|
(2)当x>15时,用含x的代数式表示水费 ;
(3)小丽家10月份水费是70元,小丽家10月份用水 m3.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解 如图1,△ABC中,沿∠BAC的平分线AB1折叠,剪掉重复部分;将余下部分沿∠B1A1C的平分线A1B2折叠,剪掉重复部分;…;将余下部分沿∠BnAnC的平分线AnBn+1折叠,点Bn与点C重合,无论折叠多少次,只要最后一次恰好重合,∠BAC是△ABC的好角.
小丽展示了确定∠BAC是△ABC的好角的两种情形.情形一:如图2,沿等腰三角形ABC顶角∠BAC的平分线AB1折叠,点B与点C重合;情形二:如图3,沿∠BAC的平分线AB1折叠,剪掉重复部分;将余下部分沿∠B1A1C的平分线A1B2折叠,此时点B1与点C重合.
探究发现
(1)△ABC中,∠B=2∠C,经过两次折叠,∠BAC是不是△ABC的好角?(填“是”或“不是”).
(2)小丽经过三次折叠发现了∠BAC是△ABC的好角,请探究∠B与∠C(不妨设∠B>∠C)之间的等量关系.根据以上内容猜想:若经过n次折叠∠BAC是△ABC的好角,则∠B与∠C(不妨设∠B>∠C)之间的等量关系为 应用提升
(3)小丽找到一个三角形,三个角分别为15°、60°、105°,发现60°和105°的两个角都是此三角形的好角. 请你完成,如果一个三角形的最小角是4°,试求出三角形另外两个角的度数,使该三角形的三个角均是此三角形的好角.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了进一步推进海南国际旅游岛建设,海口市自2012年4月1日起实施《海口市奖励旅行社开发客源市场暂行办法》,第八条规定:“旅行社引进会议规模达到200人以上,入住本市A类旅游饭店,每次会议奖励2万元;入住本市B类旅游饭店,每次会议奖励1万元.”某旅行社5月份引进符合奖励规定的会议共18次,得到28万元奖金,求此旅行社引进符合奖励规定的入住A类和B类旅游饭店的会议各多少次?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在甲、乙两名同学中选拔一人参加“中华好诗词”大赛,在相同的测试条件下,两人5次测试成绩(单位:分)如下: 甲:79,86,82,85,83
乙:88,79,90,81,72.
回答下列问题:
(1)甲成绩的平均数是 , 乙成绩的平均数是;
(2)经计算知S甲2=6,S乙2=42.你认为选拔谁参加比赛更合适,说明理由;
(3)如果从甲、乙两人5次的成绩中各随机抽取一次成绩进行分析,求抽到的两个人的成绩都大于80分的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com