
科目: 来源: 题型:
【题目】第十二届全国人大四次会议审议通过的《中华人民共和国慈善法》将于今年9月1日正式实施,为了了解居民对慈善法的知晓情况,某街道办从辖区居民中随机选取了部分居民进行调查,并将调查结果绘制成如图所示的扇形图.若该辖区约有居民9000人,则可以估计其中对慈善法“非常清楚”的居民约有人.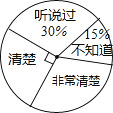
查看答案和解析>>
科目: 来源: 题型:
【题目】某校学生来自甲、乙、丙三个地区,其人数比为2:3:5,如图所示的扇形图表示上述分布情况.已知来自甲地区的为180人,则下列说法不正确的是【 】

A.扇形甲的圆心角是72°
B.学生的总人数是900人
C.丙地区的人数比乙地区的人数多180人
D.甲地区的人数比丙地区的人数少180人
查看答案和解析>>
科目: 来源: 题型:
【题目】(2017江苏省无锡市,第25题,10分)操作:“如图1,P是平面直角坐标系中一点(x轴上的点除外),过点P作PC⊥x轴于点C,点C绕点P逆时针旋转60°得到点Q.”我们将此由点P得到点Q的操作称为点的T变换.

(1)点P(a,b)经过T变换后得到的点Q的坐标为 ;若点M经过T变换后得到点N(6,![]() ),则点M的坐标为 .
),则点M的坐标为 .
(2)A是函数![]() 图象上异于原点O的任意一点,经过T变换后得到点B.
图象上异于原点O的任意一点,经过T变换后得到点B.
①求经过点O,点B的直线的函数表达式;
②如图2,直线AB交y轴于点D,求△OAB的面积与△OAD的面积之比.
查看答案和解析>>
科目: 来源: 题型:
【题目】二次函数y=2x2﹣3的图象是一条抛物线,下列关于该抛物线的说法,正确的是( )
A.抛物线开口向下
B.抛物线经过点(2,3)
C.抛物线的对称轴是直线x=1
D.抛物线与x轴有两个交点
查看答案和解析>>
科目: 来源: 题型:
【题目】学校准备从甲、乙、丙、丁四个科创小组中选出一组代表学校参加青少年科技创新大赛,各组的平时成绩的平均数 ![]() (单位:分)及方差s2如表所示:
(单位:分)及方差s2如表所示:
甲 | 乙 | 丙 | 丁 | |
| 7 | 8 | 8 | 7 |
s2 | 1 | 1.2 | 1 | 1.8 |
如果要选出一个成绩较好且状态稳定的组去参赛,那么应选的组是( )
A.甲
B.乙
C.丙
D.丁
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,抛物线与x轴交于点A(﹣5,0)和点B(3,0).与y轴交于点C(0,5).有一宽度为1,长度足够的矩形(阴影部分)沿x轴方向平移,与y轴平行的一组对边交抛物线于点P和Q,交直线AC于点M和N.交x轴于点E和F.
(1)求抛物线的解析式;
(2)当点M和N都在线段AC上时,连接MF,如果sin∠AMF= ![]() ,求点Q的坐标;
,求点Q的坐标;
(3)在矩形的平移过程中,当以点P,Q,M,N为顶点的四边形是平行四边形时,求点M的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知正方形ABCD的边长为1,点P为正方形内一动点,若点M在AB上,且满足△PBC∽△PAM,延长BP交AD于点N,连结CM.
(1)如图一,若点M在线段AB上,求证:AP⊥BN;AM=AN;
(2)①如图二,在点P运动过程中,满足△PBC∽△PAM的点M在AB的延长线上时,AP⊥BN和AM=AN是否成立?(不需说明理由)
②是否存在满足条件的点P,使得PC= ![]() ?请说明理由.
?请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】小明和爸爸从家步行去公园,爸爸先出发一直匀速前行,小明后出发.家到公园的距离为2500m,如图是小明和爸爸所走的路程s(m)与步行时间t(min)的函数图象.
(1)直接写出小明所走路程s与时间t的函数关系式;
(2)小明出发多少时间与爸爸第三次相遇?
(3)在速度都不变的情况下,小明希望比爸爸早20min到达公园,则小明在步行过程中停留的时间需作怎样的调整?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠BAC的平分线交BC于点O,OC=1,以点O为圆心OC为半径作半圆.
(1)求证:AB为⊙O的切线;
(2)如果tan∠CAO= ![]() ,求cosB的值.
,求cosB的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,直线y= ![]() x+2与双曲线相交于点A(m,3),与x轴交于点C.
x+2与双曲线相交于点A(m,3),与x轴交于点C.
(1)求双曲线解析式;
(2)点P在x轴上,如果△ACP的面积为3,求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com