
科目: 来源: 题型:
【题目】国家规定个人发表文章、出版图书所得稿费的纳税计算方法是:
①稿费不高于800元的不纳税;
②稿费高于800元,而低于4000元的应缴纳超过800元的那部分稿费的14%的税;
③稿费为4000元或高于4000元的应缴纳全部稿费的11%的税.
试根据上述纳税的计算方法作答:
(1)若王老师获得的稿费为2400元,则应纳税 元,若王老师获得的稿费为4000元,则应纳税 元;
(2)若王老师获稿费后纳税420元,求这笔稿费是多少元?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,点A,B,C,D,E,F为⊙O的六等分点,动点P从圆心O出发,沿OE弧EFFO的路线做匀速运动,设运动的时间为t,∠BPD的度数为y,则下列图象中表示y与t之间函数关系最恰当的是( )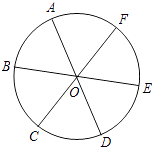
A.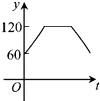
B.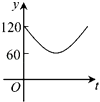
C.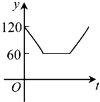
D.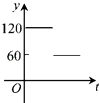
查看答案和解析>>
科目: 来源: 题型:
【题目】为了提高学生书写汉字的能力.增强保护汉字的意识,我区举办了“汉字听写大赛”,经选拔后有50名学生参加决赛,这50名学生同时听写50个汉字,若每正确听写出一个汉字得1分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
组别 | 成绩x分 | 频数(人数) |
第1组 | 25≤x<30 | 4 |
第2组 | 30≤x<35 | 6 |
第3组 | 35≤x<40 | 14 |
第4组 | 40≤x<45 | a |
第5组 | 45≤x<50 | 10 |
请结合图表完成下列各题:
(1)求表中a的值;
(2)请把频数分布直方图补充完整;
(3)若测试成绩不低于40分为优秀,则本次测试的优秀率是多少?

查看答案和解析>>
科目: 来源: 题型:
【题目】对于反比例函数![]() , 下列说法正确的是( )
, 下列说法正确的是( )
A.图象经过点(2,﹣1)
B.图象位于第二、四象限
C.当x<0时,y随x的增大而减小
D.当x>0时,y随x的增大而增大
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线 ![]() 与x轴交于点A(-2,0)、B(4,0)两点,与y轴交于点C.
与x轴交于点A(-2,0)、B(4,0)两点,与y轴交于点C.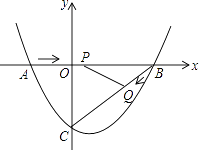
(1)求抛物线的表达式;
(2)点P从A点出发,在线段AB上以每秒3个单位长度的速度向B点运动,同时点Q从B点出发,在线段BC上以每秒1个单位长度向C点运动.其中一个点到达终点时,另一个点也停止运动.当△PBQ存在时,求运动多少秒使△PBQ的面积最大,最大面积是多少?
(3)当△PBQ的面积最大时,在BC下方的抛物线上存在点K,使 ![]() ,求K点坐标.
,求K点坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,点O是△ABC内一点,连结OB、OC,并将AB、OB、OC、AC的中点D、E、F、G依次连结,得到四边形DEFG.
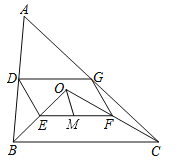
(1)求证:四边形DEFG是平行四边形;
(2)若M为EF的中点,OM=3,∠OBC和∠OCB互余,求DG的长度.
查看答案和解析>>
科目: 来源: 题型:
【题目】综合与实践
情境再现:
举世瞩目的港珠澳大桥东接香港,西接珠海、澳门,全长![]() 千米,是世界上最长的跨海大桥,被誉为“新世界七大奇迹”之一.如图,香港口岸点
千米,是世界上最长的跨海大桥,被誉为“新世界七大奇迹”之一.如图,香港口岸点![]() 至珠海口岸点
至珠海口岸点![]() 约
约![]() 千米,海底隧道
千米,海底隧道![]() 全长约
全长约![]() 千米,隧道一端的东人工岛点
千米,隧道一端的东人工岛点![]() 到香港口岸的路程为
到香港口岸的路程为![]() 千米.某一时刻,一辆穿梭巴士从香港口岸发车,沿港珠澳大桥开往珠海口岸.
千米.某一时刻,一辆穿梭巴士从香港口岸发车,沿港珠澳大桥开往珠海口岸.![]() 分钟后,一辆私家车也从香港口岸出发沿港珠澳大桥开往珠海口岸.在私家车出发的同时,一辆大客车从珠海口岸出发开往香港口岸.已知穿梭巴士的平均速度为
分钟后,一辆私家车也从香港口岸出发沿港珠澳大桥开往珠海口岸.在私家车出发的同时,一辆大客车从珠海口岸出发开往香港口岸.已知穿梭巴士的平均速度为![]() 千米/时,大客车的平均速度为
千米/时,大客车的平均速度为![]() 千米/时,私家车的平均速度为
千米/时,私家车的平均速度为![]() 千米/时.
千米/时.
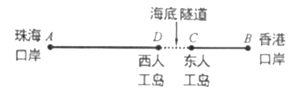
问题解决:
(1)穿梭巴士出发多长时间与大客车相遇?
(2)私家车能否在到达珠海口岸前追上穿梭巴士?说明理由;
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,点O在线段AB上,AO=2,OB=1,OC为射线,且∠BOC=60°,动点P以每秒2个单位长度的速度从点O出发,沿射线OC做匀速运动,设运动时间为t秒.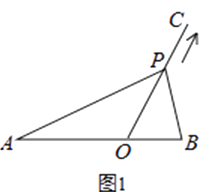
(1)当t= ![]() 秒时,则OP= , S△ABP=;
秒时,则OP= , S△ABP=;
(2)当△ABP是直角三角形时,求t的值;
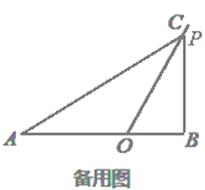
(3)如图2,当AP=AB时,过点A作AQ∥BP,并使得∠QOP=∠B,求证:AQ·BP=3.为了证明AQ·BP=3,小华同学尝试过O点作OE∥AP交BP于点E.试利用小华同学给我们的启发补全图形并证明AQ·BP=3.
查看答案和解析>>
科目: 来源: 题型:
【题目】甲、乙两家草莓采摘园的草莓品质相同,销售价格也相同.“五一期间”,两家均推出了优惠方案,甲采摘园的优惠方案是:游客进园需购买50元的门票,采摘的草莓六折优惠;乙采摘园的优惠方案是:游客进园不需购买门票,采摘园的草莓超过一定数量后,超过部分打折优惠.优惠期间,设某游客的草莓采摘量为x(千克),在甲采摘园所需总费用为![]() (元),在乙采摘园所需总费用为
(元),在乙采摘园所需总费用为![]() (元),图中折线OAB表示
(元),图中折线OAB表示![]() 与x之间的函数关系.
与x之间的函数关系.
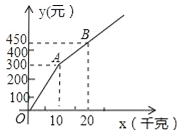
(1)甲、乙两采摘园优惠前的草莓销售价格是每千克 元;
(2)求![]() 、
、![]() 与x的函数表达式;
与x的函数表达式;
(3)在图中画出![]() 与x的函数图象,并写出选择甲采摘园所需总费用较少时,草莓采摘量x的范围.
与x的函数图象,并写出选择甲采摘园所需总费用较少时,草莓采摘量x的范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:抛物线 ![]() 与
与 ![]() 轴分别交于点A(-3,0),B(m,0).将y1向右平移4个单位得到y2 .
轴分别交于点A(-3,0),B(m,0).将y1向右平移4个单位得到y2 .
(1)求b的值;
(2)求抛物线y2的表达式;
(3)抛物线y2与 ![]() 轴交于点D,与
轴交于点D,与 ![]() 轴交于点E、F(点E在点F的左侧),记抛物线在D、F之间的部分为图象G(包含D、F两点),若直线
轴交于点E、F(点E在点F的左侧),记抛物线在D、F之间的部分为图象G(包含D、F两点),若直线 ![]() 与图象G有一个公共点,请结合函数图象,求直线
与图象G有一个公共点,请结合函数图象,求直线 ![]() 与抛物线y2的对称轴交点的纵坐标t的值或取值范围.
与抛物线y2的对称轴交点的纵坐标t的值或取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com