
科目: 来源: 题型:
【题目】如图,经过坐标原点的抛物线C1:y=ax2+bx与x轴的另一交点为M,它的顶点为点A,将C1绕原点旋转180°,得到抛物线C2 , C2与x轴的另一交点为N,顶点为点B,连接AM,MB,BN,NA,当四边形AMBN恰好是矩形时,则b的值( )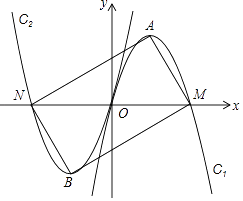
A.2 ![]()
B.﹣2 ![]()
C.2 ![]()
D.﹣2 ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,抛物线y=x2+bx+c与x轴交于点A,B,与y轴交于点C,其中点A在y轴的左侧,点C在x轴的下方,且OA=OC=5.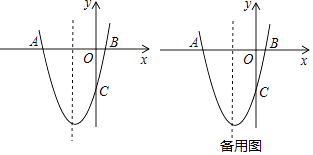
(1)求抛物线对应的函数解析式;
(2)点P为抛物线对称轴上的一动点,当PB+PC的值最小时,求点P的坐标;
(3)在(2)条件下,点E为抛物线的对称轴上的动点,点F为抛物线上的动点,以点P、E、F为顶点作四边形PEFM,当四边形PEFM为正方形时,请直接写出坐标为整数的点M的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】根据要求回答问题:
(1)发现
如图1,直线l1∥l2 , l1和l2的距离为d,点P在l1上,点Q在l2上,连接PQ,填空:PQ长度的最小值为.
(2)应用
如图2,在四边形ABCD中,DC∥AB,AD⊥AB,DC=2,AD=4,AB=6,点M在线段AD上,AM=3MD,点N在直线BC上,连接MN,求MN长度的最小值
(3)拓展
如图3,在四边形ABCD中,DC∥AB,AD⊥AB,DC=2,AD=4,AB=6,点M在线段AD上任意一点,连接MC并延长到点E,使MC=CE,以MB和ME为边作平行四边形MBNE,请直接写出线段MN长度的最小值
查看答案和解析>>
科目: 来源: 题型:
【题目】如果关于x的一元二次方程ax2+bx+c=0有两个实数根,且其中一个根为另一个根的2倍,则称这样的方程为“倍根方程”,以下关于“倍根方程”的说法:①方程x2-3x+2=0是“倍根方程”;②若(x-2)(mx+n)=0是“倍根方程”,则4m2+5mn+n2=0;③若pq=2,则关于x的方程px2+3x+q=0是“倍根方程”;④若方程ax2+bx+c=0是“倍根方程”,且5a+b=0,则方程ax2+bx+c=0的一个根为![]() .其中正确的是____(填序号).
.其中正确的是____(填序号).
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形ABCD的顶点A、D在坐标轴上,其坐标分别为(2,0),(0,4),对角线AC⊥x轴. 
(1)求直线DC对应的函数解析式
(2)若反比例函数y= ![]() (k>0)的图象经过DC的中点M,请判断这个反比例函数的图象是否经过点B,并说明理由.
(k>0)的图象经过DC的中点M,请判断这个反比例函数的图象是否经过点B,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某厂生产一种工具,据市场调查,若按每个工具280元销售时,每月可销售300个,若销售单价每降低1元,每月可多售出2个,据统计,每个工具的固定成本Q(元)与月销售y(个)满足如下关系:
月销量y(个) | 100 | 160 | 240 | 320 |
每个工具的固定成本Q(元) | 96 | 60 | 40 | 30 |
(1)写出月产销量y(个)与销售单价x(元)之间的函数关系式;
(2)求每个玩具的固定成本Q(元)与月产销量y(个)之间的函数关系式;
(3)若该厂这种玩具的月产销量不超过400个,则每个玩具的固定成本至少为多少元?销售单价最低为多少元?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,甲乙两人在游泳池A处发现游泳池中的P处有人求救,甲立即跳入池中去救人,速度为1米/秒,乙以3.5米/秒的速度沿游泳池边跑到距A不远处的B处,捡起一个游泳圈再跳入池中去救人,甲游了20秒到达P处,两秒后乙到达P处.若∠PAB与∠PBC互余,且cos∠PBC= ![]() ,求乙的游泳速度.
,求乙的游泳速度. 
查看答案和解析>>
科目: 来源: 题型:
【题目】四个全等的直角三角形按图示方式围成正方形ABCD,过各较长直角边的中点作垂线,围成面积为![]() 的小正方形EFGH,已知AM为Rt△ABM较长直角边,AM=
的小正方形EFGH,已知AM为Rt△ABM较长直角边,AM=![]() EF,则正方形ABCD的面积为( )
EF,则正方形ABCD的面积为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com