
【题目】如图,抛物线y=x2+bx+c与x轴交于点A,B,与y轴交于点C,其中点A在y轴的左侧,点C在x轴的下方,且OA=OC=5.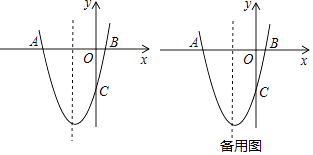
(1)求抛物线对应的函数解析式;
(2)点P为抛物线对称轴上的一动点,当PB+PC的值最小时,求点P的坐标;
(3)在(2)条件下,点E为抛物线的对称轴上的动点,点F为抛物线上的动点,以点P、E、F为顶点作四边形PEFM,当四边形PEFM为正方形时,请直接写出坐标为整数的点M的坐标.
【答案】
(1)解:由题意,可得A(﹣5,0),C(0,﹣5).
∵抛物线y=x2+bx+c过点A,点C,
∴ ![]() ,
,
解得 ![]() ,
,
∴抛物线对应的函数解析式为y=x2+4x﹣5;
(2)解:∵y=x2+4x﹣5=(x+2)2﹣9,
∴对称轴是直线x=﹣2.
∵抛物线y=x2+4x﹣5与x轴交于点A,B,
∴点A,B关于直线x=﹣2对称.
连结AC,交对称轴于点P,此时PB+PC的值最小.

设直线AC的解析式为y=mx+n,
则 ![]() ,解得
,解得 ![]() ,
,
∴直线AC的解析式为y=﹣x﹣5,
当x=﹣2时,y=﹣3,
∴点P的坐标为(﹣2,﹣3)
(3)解:在(2)条件下,点P的坐标为(﹣2,﹣3).
设F(x,x2+4x﹣5),
∵四边形PEFM为正方形,
∴E(﹣2,x2+4x﹣5),M(x,﹣3),PM=PE,
∴|x+2|=|x2+4x﹣5+3|,
∴x2+4x﹣2=x+2,或x2+4x﹣2=﹣x﹣2,
整理得x2+3x﹣4=0,或x2+5x=0,
解得x1=﹣4,x2=1,x3=0,x4=﹣5,
∴M(﹣4,﹣3)或M(1,﹣3)或M(0,﹣3)或M(﹣5,﹣3)
【解析】(1)由题意,可得A(﹣5,0),C(0,﹣5).把点A,C的坐标代入y=x2+bx+c,得到关于b、c的二元一次方程组,解方程组即可求出抛物线的函数解析式;(2)利用配方法求出抛物线的对称轴是直线x=﹣2.由抛物线y=x2+4x﹣5与x轴交于点A,B,得出点A,B关于直线x=﹣2对称.连结AC,交对称轴于点P,根据两点之间线段最短可知此时PB+PC的值最小.利用待定系数法求出直线AC的解析式为y=﹣x﹣5,把x=﹣2代入,求出y=﹣3,进而得出点P的坐标;(3)在(2)条件下,点P的坐标为(﹣2,﹣3).设F(x,x2+4x﹣5),根据正方形的性质可得E(﹣2,x2+4x﹣5),M(x,﹣3),PM=PE,根据两点间的距离公式列出方程|x+2|=|x2+4x﹣5+3|,解方程即可求解.
【考点精析】本题主要考查了二次函数的性质的相关知识点,需要掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小才能正确解答此题.


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案科目:初中数学 来源: 题型:
【题目】2008年奥运会期间,一辆大巴车在一条南北方向的道路上来回运送旅客,某一天早晨该车从A地出发,晚上到达B地,预定向北为正方向,当天行驶记录如下(单位:千米)
+18,-9,+7,-14,-6,+13,-6,-8
请你根据计算回答下列问题:
(1)B地在A地何方?相距多少千米?
(2)该车这一天共行驶多少千米?
(3)若该车每千米耗油0.4升,这一天共耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解全校2000名学生每周去图书馆时间的情况,随机调查了其中的100名学生,对这100名学生每周去图书馆的时间x(单位:小时)进行了统计.根据所得数据绘制了一幅不完整的统计图,并知道每周去图书馆的时间在6≤x<8小时的学生人数占20%.根据以上信息及统计图解答下列问题: 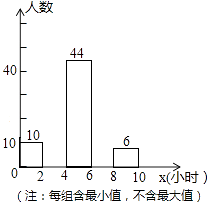
(1)本次调查属于调查,样本容量是;
(2)请补全频数分布直方图中空缺的部分;
(3)若从这100名学生中随机抽取1名学生,求抽取的这个学生每周去图书馆的时间恰好在8﹣10小时的概率;
(4)估计全校学生每周去图书馆的时间不少于6小时的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形ABCD的顶点A、D在坐标轴上,其坐标分别为(2,0),(0,4),对角线AC⊥x轴. 
(1)求直线DC对应的函数解析式
(2)若反比例函数y= ![]() (k>0)的图象经过DC的中点M,请判断这个反比例函数的图象是否经过点B,并说明理由.
(k>0)的图象经过DC的中点M,请判断这个反比例函数的图象是否经过点B,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A在数轴上对应的数为a,点B在数轴上对应的数为b,且|a+3|+|b-2|=0,A,B 之间的距离记为|AB|.请回答问题:
(1)直接写出a,b, |AB|的值. a= ,b = , |AB|= ;
(2)设点P在数轴上对应的数为x,当|PA|-|PB|=2时,求x的值;
(3)若点P在点A的左侧,M、N分别是PA、PB的中点.当点P在点A的左侧移动时,式子|PN|-|PM|的值是否发生改变?若不变,请求出其值;若发生变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,以点A为圆心,一定长为半径作圆弧,分别交AD、AB于点E、F;再分别以点E、F为圆心,大于 ![]() EF的长为半径作弧,两弧交于点G;作射线AG,交边CD于点H.若AB=6,AD=4,则四边形ABCH的周长与三角形ADH的周长之差为( )
EF的长为半径作弧,两弧交于点G;作射线AG,交边CD于点H.若AB=6,AD=4,则四边形ABCH的周长与三角形ADH的周长之差为( ) 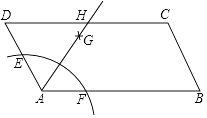
A.4
B.5
C.6
D.7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一盒中有x个黑球和2个白球,这些球除颜色外无其他差别.若从盒中随机取一个球,黑球的概率是 ![]() .
.
(1)填空:x=;
(2)从该盒子中随机摸出一个球,记下颜色后,不放回,再从该盒子中摸出一个球记下颜色,请用画树状图或列表求两次摸出的球的颜色都是白色的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了加强公民节水意识,合理利用水资源,某市采用价格调控手段达到节约用水的目的,规定:每户居民每月用水不超过15m3时,按基本价格收费;超过15m3时,不超过的部分仍按基本价格收费,超过的部分要加价收费,该市某户居民今年4、5月份的用水量和水费如表所示:
月份 | 用水量/m3 | 水费/元 |
4 | 16 | 50 |
5 | 20 | 70 |
(1)求该市居民用水的两种收费价格;
(2)若该居民6月份交水费80元,那么该居民这个月水量为m3 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com