
科目: 来源: 题型:
【题目】某苹果生产基地,用30名工人进行采摘或加工苹果 ,每名工人只能做其中一项工作.苹果的销售方式有两种:一种是可以直接出售;另一种是可以将采摘的苹果加工成罐头出售.直接出售每吨获利4 000元;加工成罐头出售每吨获利10 000元.采摘的工人每人可采摘苹果0.4吨;加工罐头的工人每人可加工0.3吨.设有x名工人进行苹果采摘,全部售出后,总利润为y元.
(1)求y与x的函数关系式;
(2)如何分配工人才能获利最大?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在ABCD中,延长CD到E,使DE=CD,连接BE交AD于点F,交AC于点G.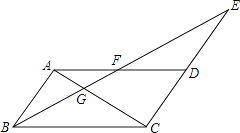
(1)求证:AF=DF;
(2)若BC=2AB,DE=1,∠ABC=60°,求FG的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】某学校有1500名学生参加首届“我爱我们的课堂”为主题的图片制作比赛,赛后随机抽取部分参赛学生的成绩进行整理并制作成图表如图:
分数段 | 频数 | 频率 |
60≤x<70 | 40 | 0.40 |
70≤x<80 | 35 | b |
80≤x<90 | a | 0.15 |
90≤x<100 | 10 | 0.10 |
频率分布统计表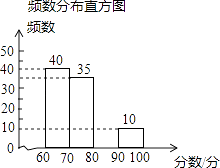
请根据上述信息,解答下列问题:
(1)分别求出a、b的值;
(2)请补全频数分布直方图;
(3)如果将比赛成绩80分以上(含80分)定为优秀,那么优秀率是多少?并且估算该校参赛学生获得优秀的人数.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,直线y= ![]() x与双曲线y=
x与双曲线y= ![]() 相交于A、B两点,BC⊥x轴于点C(﹣4,0).
相交于A、B两点,BC⊥x轴于点C(﹣4,0).
(1)求A、B两点的坐标及双曲线的解析式;
(2)若经过点A的直线与x轴的正半轴交于点D,与y轴的正半轴交于点E,且△AOE的面积为10,求CD的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】某农场急需铵肥8吨,在该农场南北方向分别有一家化肥公司A、B,A公司有铵肥3吨,每吨售价750元;B公司有铵肥7吨,每吨售价700元,汽车每千米的运输费用b(单位:元/千米)与运输重量a(单位:吨)的关系如图所示.

(1)根据图象求出b关于a的函数解析式(包括自变量的取值范围);
(2)若农场到B公司的路程是农场到A公司路程的2倍,农场到A公司的路程为m千米,设农场从A公司购买x吨铵肥,购买8吨铵肥的总费用为y元(总费用=购买铵肥费用+运输费用),求出y关于x的函数解析式(m为常数),并向农场建议总费用最低的购买方案.
查看答案和解析>>
科目: 来源: 题型:
【题目】下面是某同学对多项式(x2-4x+2)(x2-4x+6)+4进行因式分解的过程.
解:设x2-4x=y
原式=(y+2)(y+6)+4 (第一步)
=y2+8y+16 (第二步)
=(y+4)2(第三步)
=(x2-4x+4)2(第四步)
回答下列问题:
(1)该同学第二步到第三步运用了因式分解的_______.
A.提取公因式 |
B.平方差公式 |
C.两数和的完全平方公式 |
D.两数差的完全平方公式 |
(2)该同学因式分解的结果是否彻底?________.(填“彻底”或“不彻底”)若不彻底,请直接写出因式分解的最后结果_________ .
(3)请你模仿以上方法尝试对多项式(x2-2x)(x2-2x+2)+1进行因式分解.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知△ABC,且∠ACB=90°.
(1)请用直尺和圆规按要求作图(保留作图痕迹,不写作法和证明):
①以点A为圆心,BC边的长为半径作⊙A;
②以点B为顶点,在AB边的下方作∠ABD=∠BAC.
(2)请判断直线BD与⊙A的位置关系(不必证明).
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,将一张矩形纸板按图中虚线裁剪成九块,其中有两块是边长都为![]() 的大正方形,两块是边长都为
的大正方形,两块是边长都为![]() 的小正方形,五块是长为
的小正方形,五块是长为![]() 、宽为
、宽为![]() 的全等小矩形,且
的全等小矩形,且![]() >
> ![]() .(以上长度单位:cm)
.(以上长度单位:cm)
(1)观察图形,可以发现代数式![]() 可以因式分解为 ;
可以因式分解为 ;
(2)若每块小矩形的面积为10![]() ,四个正方形的面积和为58
,四个正方形的面积和为58![]() ,试求图中所有裁剪线(虚线部分)长之和.
,试求图中所有裁剪线(虚线部分)长之和.

查看答案和解析>>
科目: 来源: 题型:
【题目】全球气候变暖导致-些冰川融化并消失,在冰川|消失12年后,一种低等植物苔藓,就开始在岩石上生长,每一个苔藓都会长成近似的圆形,苔藓的直径和其生长年限近似地满足如下的关系式:d=7![]() (t≥12),其中d表示苔藓的直径,单位是厘米,t代表冰川消失的时间(单位:年)。
(t≥12),其中d表示苔藓的直径,单位是厘米,t代表冰川消失的时间(单位:年)。
(1)计算冰川消失16年后苔藓的直径为多少厘米?
(2)如果测得一些苔藓的直径是35厘米,问冰川约是在多少年前消失的?
查看答案和解析>>
科目: 来源: 题型:
【题目】(10分)某地区为了鼓励市民节约用水,计划实行生活用水按阶梯式水价计费,每月用水量不超过10吨(含10吨)时,每吨按基础价收费;每月用水量超过10吨时,超过的部分每吨按调节价收费.例如,第一个月用水16吨,需交水费17.8元,第二个月用水20吨,需交水费23元.
(1)求每吨水的基础价和调节价;
(2)设每月用水量为n吨,应交水费为m元,写出m与n之间的函数解析式;
(3)若某月用水12吨,应交水费多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com