
科目: 来源: 题型:
【题目】如图,直线AB、CD相交于点O,∠BOM=90°,∠DON=90°.
(1)若∠COM=∠AOC,求∠AOD的度数;
(2)若∠COM=![]() ∠BOC,求∠AOC和∠MOD.
∠BOC,求∠AOC和∠MOD.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,△ABC中,∠A=36°,AB=AC,BD平分∠ABC,DE∥BC,则图中等腰三角形的个数( )
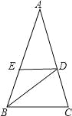
A. 1个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目: 来源: 题型:
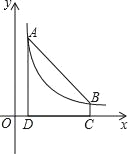
【题目】如图,点A(m,6),B(n,1)在反比例函数图象上,AD⊥x轴于点D,BC⊥x轴于点C,DC=5.
(1)求m,n的值并写出反比例函数的表达式;
(2)连结AB,在线段DC上是否存在一点E,使△ABE的面积等于5?若存在,求出点E的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,直线EF,CD相交于点0,OA⊥OB,且OC平分∠AOF,
(1)若∠AOE=40°,求∠BOD的度数;
(2)若∠AOE=α,求∠BOD的度数;(用含α的代数式表示)
(3)从(1)(2)的结果中能看出∠AOE和∠BOD有何关系?

查看答案和解析>>
科目: 来源: 题型:
【题目】反比例函数![]() 和
和![]() (k≠0)在第一象限内的图象如图所示,点P在
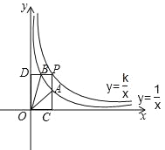
(k≠0)在第一象限内的图象如图所示,点P在![]() 的图象上,PC⊥x轴,垂足为C,交
的图象上,PC⊥x轴,垂足为C,交![]() 的图象于点A,PD⊥y轴,垂足为D,交
的图象于点A,PD⊥y轴,垂足为D,交![]() 的图象于点B.已知点A(m,1)为线段PC的中点.
的图象于点B.已知点A(m,1)为线段PC的中点.
(1)求m和k的值;
(2)求四边形OAPB的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】自2016年国庆后,许多高校均投放了使用手机就可随用的共享单车.某运营商为提高其经营的A品牌共享单车的市场占有率,准备对收费作如下调整:一天中,同一个人第一次使用的车费按0.5元收取,每增加一次,当次车费就比上次车费减少0.1元,第6次开始,当次用车免费.具体收费标准如下:
使用次数 | 0 | 1 | 2 | 3 | 4 | 5(含5次以上) |
累计车费 | 0 | 0.5 | 0.9 | a | b | 1.5 |
同时,就此收费方案随机调查了某高校100名师生在一天中使用A品牌共享单车的意愿,得到如下数据:
使用次数 | 0 | 1 | 2 | 3 | 4 | 5 |
人数 | 5 | 15 | 10 | 30 | 25 | 15 |
(Ⅰ)写出a,b的值;
(Ⅱ)已知该校有5000名师生,且A品牌共享单车投放该校一天的费用为5800元.试估计:收费调整后,此运营商在该校投放A品牌共享单车能否获利?说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】反比例函数![]() 的图象的一支在第一象限,A(﹣1,a)、B(﹣3,b)均在这个函数的图象上.
的图象的一支在第一象限,A(﹣1,a)、B(﹣3,b)均在这个函数的图象上.
(1)图象的另一支位于什么象限?常数n的取值范围是什么?
(2)试比较a、b的大小;
(3)作AC⊥x轴于点C,若△AOC的面积为5,求这个反比例函数的表达式.
查看答案和解析>>
科目: 来源: 题型:
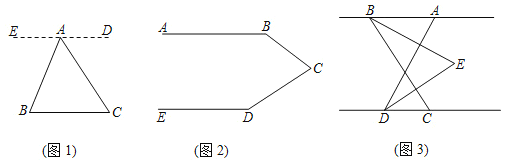
【题目】(1)如图1,已知点![]() 是
是![]() 外一点,连接
外一点,连接![]() ,
,![]() .求
.求![]() 的度数.
的度数.
请补充下面的推理过程:
解:过点![]() 作
作![]() ,所以
,所以![]() ,
,![]() _______.
_______.
又因为![]() °,所以
°,所以![]() .
.
(2)如图2,已知![]() ,借鉴(1)的方法,求
,借鉴(1)的方法,求![]() 的度数;
的度数;
(3)如图3,已知![]() ,
,![]() .
.![]() ,
,![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,
,![]() ,
,![]() 所在的直线交于点
所在的直线交于点![]() ,点
,点![]() 在
在![]() 与
与![]() 两条平行线之间,借鉴(1)的方法,求
两条平行线之间,借鉴(1)的方法,求![]() 的度数.
的度数.
查看答案和解析>>
科目: 来源: 题型:
【题目】“五一”期间,甲、乙两家商店以同样价格销售相同的商品,两家优惠方案分别为:甲店一次性购物中超过200元后的价格部分打七折;乙店一次性购物中超过500元后的价格部分打五折,设商品原价为x元(x≥0),购物应付金额为y元.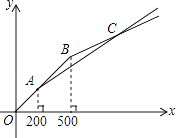
(1)求在甲商店购物时y与x之间的函数关系;
(2)两种购物方式对应的函数图象如图所示,求交点C的坐标;
(3)根据图象,请直接写出“五一”期间选择哪家商店购物更优惠.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com