
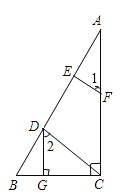
【题目】如图,已知DG⊥BC,AC⊥BC,EF⊥AB,∠1=∠2,求证:CD⊥AB
【答案】见解析;
【解析】
灵活运用垂直的定义,注意由垂直可得90°角,由90°角可得垂直,结合平行线的判定和性质,只要证得∠ADC=90°,即可得CD⊥AB.
证明:∵ DG⊥BC,AC⊥BC(已知),
∴ ∠DGB=∠ACB=90°(垂直的定义),
∴ DG∥AC(同位角相等,两直线平行).
∴ ∠2=∠ACD(两直线平行,内错角相等).
∵ ∠1=∠2(已知),∴ ∠1=∠ACD(等量代换),
∴ EF∥CD(同位角相等,两直线平行).
∴ ∠AEF=∠ADC(两直线平行,同位角相等).
∵ EF⊥AB(已知),∴ ∠AEF=90°(垂直的定义),
∴ ∠ADC=90°(等量代换).
∴ CD⊥AB(垂直的定义).


科目:初中数学 来源: 题型:
【题目】如图是一个平面直角坐标系,按要求完成下列各小题.
(1)写出图中的六边形ABCDEF顶点在坐标轴上的点的坐标;
(2)说明点B与点C的纵坐标有什么特点?线段BC与x轴有怎样的位置关系?
(3)写出点E关于y轴的对称点E′的坐标,并指出点E′与点C有怎样的位置关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列解答过程:如图甲,AB∥CD,探索∠P与∠A,∠C之间的关系.
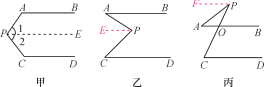
解:过点P作PE∥AB.
∵AB∥CD,
∴PE∥AB∥CD(平行于同一条直线的两条直线互相平行).
∴∠1+∠A=180°(两直线平行,同旁内角互补),
∠2+∠C=180°(两直线平行,同旁内角互补).
∴∠1+∠A+∠2+∠C=360°.
又∵∠APC=∠1+∠2,
∴∠APC+∠A+∠C=360°.
如图乙和图丙,AB∥CD,请根据上述方法分别探索两图中∠P与∠A,∠C之间的关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
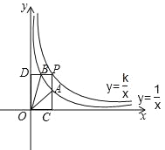
【题目】反比例函数![]() 和
和![]() (k≠0)在第一象限内的图象如图所示,点P在
(k≠0)在第一象限内的图象如图所示,点P在![]() 的图象上,PC⊥x轴,垂足为C,交
的图象上,PC⊥x轴,垂足为C,交![]() 的图象于点A,PD⊥y轴,垂足为D,交
的图象于点A,PD⊥y轴,垂足为D,交![]() 的图象于点B.已知点A(m,1)为线段PC的中点.
的图象于点B.已知点A(m,1)为线段PC的中点.
(1)求m和k的值;
(2)求四边形OAPB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果批发市场香蕉的价格如下表
购买香蕉数(千克) | 不超过20千克 | 20千克以上但不超过40千克 | 40千克以上 |
每千克的价格 | 6元 | 5元 | 4元 |
张强两次共购买香蕉50千克,已知第二次购买的数量多于第一次购买的数量,共付出264元,请问张强第一次,第二次分别购买香蕉多少千克?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BF,DE相交于点A,BG交BF于点B,交AC于点C.
(1)指出DE,BC被BF所截形成的同位角、内错角、同旁内角;
(2)指出DE,BC被AC所截形成的内错角、同旁内角;
(3)指出FB,BC被AC所截形成的内错角、同旁内角.

查看答案和解析>>
科目:初中数学 来源: 题型:
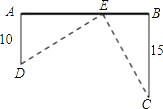
【题目】如图,在笔直的铁路上A、B两点相距25km,C、D为两村庄,DA=10km,CB=15km,DA⊥AB于A,CB⊥AB于B,现要在AB上建一个中转站E,使得C、D两村到E站的距离相等.求E应建在距A多远处?
查看答案和解析>>
科目:初中数学 来源: 题型:
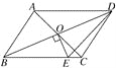
【题目】如图,平行四边形ABCD的对角线相交于点O,且AB≠AD,过O作OE⊥BD交BC于点E.若△CDE的周长为10,则AB+AD的值是( )
A. 10
B. 15
C. 25
D. 30
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com