（1）小亮行走的总路程是___________m，他途中休息了_____________min；

（2）①当50＜x＜80时，求y与x的函数关系式；②当小颖到达缆车终点时，小亮离缆车终点的路程是多少？

（1）如果y关于x的函数是一次函数，求这个函数解析式（不要求写出自变量的取值范围）

（2）在（1）的条件下，如果货车的行驶速度和每小时的耗油量都不变，货车行驶4小时后到达C处，C的前方12千米的D处有一加油站，那么在D处至少加多少升油，才能使货车到达B处卸货后能顺利返回会D处加油？（根据驾驶经验，为保险起见，油箱内剩余油量应随时不少于10升）

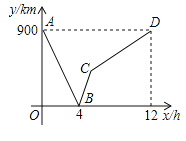
（1）甲、乙两地之间的距离为 千米；图中点B的实际意义是 ；

（2）求线段BC所表示的y与x之间的函数关系式，并写出自变量x的取值范围；

（3）若第二列快车也从甲地出发驶往乙地，速度与第一列快车相同．在第一列快车与慢车相遇30分钟后，第二列快车与慢车相遇．求第二列快车比第一列快车晚出发多少小时？

（1）求A种，B种树木每棵各多少元？

（2）因布局需要，购买A种树木的数量不少于B种树木数量的3倍．学校与中标公司签订的合同中规定：在市场价格不变的情况下（不考虑其他因素），实际付款总金额按市场价九折优惠，请设计一种购买树木的方案，使实际所花费用最省，并求出最省的费用．

【题目】已知：如图，在平面直角坐标系xoy中，一次函数y= x+3的图象与x轴和y轴交于A、B两点，将△AOB绕点O顺时针旋转90°后得到△A′OB′．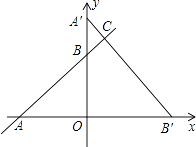

（1）求直线A′B′的解析式；
（2）若直线A′B′与直线AB相交于点C，求S△ABC：S△ABO的值．

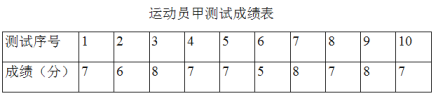
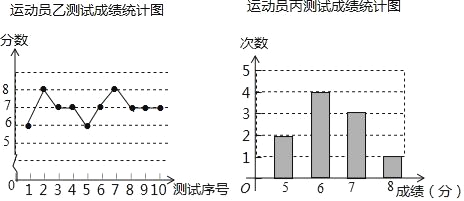
（1）写出运动员甲测试成绩的众数和中位数；

（2）在他们三人中选择一位垫球成绩优秀且较为稳定的接球能手作为自由人，你认为选谁更合适？为什么？（参考数据：三人成绩的方差分别为S甲2＝0.8、S乙2＝0.4、S丙2＝0.8）

（1）求证：四边形ABCD是矩形；

（2）若AB=2，求△OEC的面积．

【题目】在平面直角坐标系中（单位长度为），已知点，，且．

（1）求，的值；

（2）若点是第一象限内一点，且轴，点到轴的距离为4，过点作轴的平行线，与轴交于点，点从点处出发，以每秒的速度沿直线向左移动，点从原点同时出发，以每秒的速度沿轴向右移动．

①经过几秒平行于轴？

②若某一时刻以，，，为顶点的四边形的面积是，求此时点的坐标．

【题目】七年级（2）班的同学组织到人民公园游玩，张明、王励、李华三位同学和其他同学走散了，同学们已到中心广场，他们三个对着景区示意图在电话中向在中心广场的同学们说他们的位置，张明说他的坐标是，王励说他的坐标是，李华说他的坐标是．

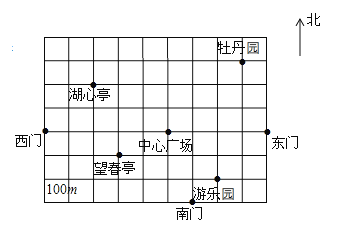
（1）请你根据题目条件，在图中画出平面直角坐标系；

（2）写出这三位同学所在的位置；

（3）写出除了这三位同学所在位置外，图中其余两个景点的坐标．

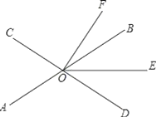
（1）若∠AOC=70°，∠DOF=90°，求∠EOF的度数；

（2）若OF平分∠COE，∠BOF=15°，若设∠AOE=x°．

①用含x的代数式表示∠EOF；

②求∠AOC的度数．