
科目: 来源: 题型:
【题目】如图,在正方形ABCD中,△ABE和△CDF为直角三角形,∠AEB=∠CFD=90°,AE=CF=5,BE=DF=12,则EF的长是( ) 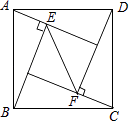
A.7
B.8
C.7 ![]()
D.7 ![]()
查看答案和解析>>
科目: 来源: 题型:
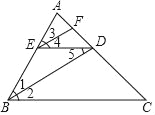
【题目】如图,BD是∠ABC的平分线,ED∥BC,∠4=∠5,则EF也是∠AED的平分线.完成下列推理过程:
证明:∵BD是∠ABC的平分线(已知)
∴∠1=∠2(角平分线定义)
∵ED∥BC(已知)
∴∠5=∠2( )
∴∠1=∠5(等量代换)
∵∠4=∠5(已知)
∴EF∥ ( )
∴∠3=∠1( )
∴∠3=∠4(等量代换)
∴EF是∠AED的平分线(角平分线定义)
查看答案和解析>>
科目: 来源: 题型:
【题目】某超市预测某饮料有发展前途,用1600元购进一批饮料,面市后果然供不应求,又用6000元购进这批饮料,第二批饮料的数量是第一批的3倍,但单价比第一批贵2元.
(1)第一批饮料进货单价多少元?
(2)若二次购进饮料按同一价格销售,两批全部售完后,获利不少于1200元,那么销售单价至少为多少元?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的三个顶点的坐标分别是:A(2,2),B(1,0),C(3,1).
(1)画出△ABC关于x轴对称的△A′B′C′,并求出点A′、B′、C′的坐标.
(2)在坐标平面内是否存在点D,使得△COD为等腰三角形?若存在,直接写出点D的坐标(找出满足条件的两个点即可);若不存在,请说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】某车间有技术工人85人,平均每天每人可加工甲种部件16个或乙种部件10个,2个甲种部件和3个乙种部件配成一套,问加工甲、乙两种部件各安排多少人才能使每天加工的两种部件刚好配套?并求出加工了多少套?
查看答案和解析>>
科目: 来源: 题型:
【题目】在直角梯形![]() 中,
中,![]() ,
,![]() 为
为![]() 边上一点,
边上一点,![]() ,且
,且![]() .连接
.连接![]() 交对角线
交对角线![]() 于
于![]() ,连接
,连接![]() .下列结论:
.下列结论:

①![]() ;②
;②![]() 为等边三角形;
为等边三角形;
③![]() ; ④
; ④![]() .其中结论正确的是
.其中结论正确的是
A.只有①② | B.只有①②④ |
C.只有③④ | D.①②③④ |
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读理(解析)
提出问题:如图1,在四边形ABCD中,P是AD边上任意一点,△PBC与△ABC和△DBC的面积之间有什么关系?探究发现:为了解决这个问题,我们可以先从一些简单的、特殊的情形入手:
当AP=![]() AD时(如图2):
AD时(如图2):
∵AP=![]() AD,△ABP和△ABD的高相等,
AD,△ABP和△ABD的高相等,
∴S△ABP=![]() S△ABD,
S△ABD,
∵PD=AD﹣AP=![]() AD,△CDP和△CDA的高相等
AD,△CDP和△CDA的高相等
∴S△CDP=![]() S△CDA,
S△CDA,
∴S△PBC=S四边形ABCD﹣S△ABP﹣S△CDP=S四边形ABCD﹣![]() S△ABD﹣
S△ABD﹣![]() S△CDA,
S△CDA,
=S四边形ABCD﹣![]() (S四边形ABCD﹣S△DBC)﹣
(S四边形ABCD﹣S△DBC)﹣![]() (S四边形ABCD﹣S△ABC)=
(S四边形ABCD﹣S△ABC)=![]() S△DBC+
S△DBC+![]() S△ABC.
S△ABC.
(1)当AP=![]() AD时,探求S△PBC与S△ABC和S△DBC之间的关系式并证明;
AD时,探求S△PBC与S△ABC和S△DBC之间的关系式并证明;
(2)当AP=![]() AD时,S△PBC与S△ABC和S△DBC之间的关系式为: ;
AD时,S△PBC与S△ABC和S△DBC之间的关系式为: ;
(3)一般地,当AP=![]() AD(n表示正整数)时,探求S△PBC与S△ABC和S△DBC之间的关系为: ;
AD(n表示正整数)时,探求S△PBC与S△ABC和S△DBC之间的关系为: ;
(4)当AP=![]() AD(0≤
AD(0≤![]() ≤1)时,S△PBC与S△ABC和S△DBC之间的关系式为: .
≤1)时,S△PBC与S△ABC和S△DBC之间的关系式为: .

查看答案和解析>>
科目: 来源: 题型:
【题目】问题:如图(1),点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,试判断BE、EF、FD之间的数量关系.
【发现证明】小聪把△ABE绕点A逆时针旋转90°至△ADG,从而发现EF=BE+FD,请你利用图(1)证明上述结论.
【类比引申】如图(2),四边形ABCD中,∠BAD≠90°,AB=AD,∠B+∠D=180°,点E、F分别在边BC、CD上,则当∠EAF与∠BAD满足 关系时,仍有EF=BE+FD;请证明你的结论.
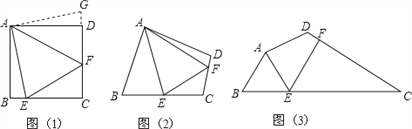
【探究应用】如图(3),在某公园的同一水平面上,四条通道围成四边形ABCD.已知AB=AD=80米,∠B=60°,∠ADC=120°,∠BAD=150°,道路BC、CD上分别有景点E、F,且AE⊥AD,DF=40(![]() ﹣1)米,现要在E、F之间修一条笔直道路,求这条道路EF的长.(结果取整数,参考数据:
﹣1)米,现要在E、F之间修一条笔直道路,求这条道路EF的长.(结果取整数,参考数据: ![]() =1.41,
=1.41, ![]() =1.73)
=1.73)
查看答案和解析>>
科目: 来源: 题型:
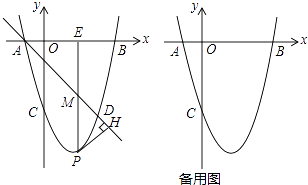
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,点A的坐标为(﹣1,0),且OC=OB,tan∠ACO= ![]() .
.
(1)求抛物线的解析式;
(2)若点D和点C关于抛物线的对称轴对称,直线AD下方的抛物线上有一点P,过点P作PH⊥AD于点H,作PM平行于y轴交直线AD于点M,交x轴于点E,求△PHM的周长的最大值;
(3)在(2)的条件下,以点E为端点,在直线EP的右侧作一条射线与抛物线交于点N,使得∠NEP为锐角,在线段EB上是否存在点G,使得以E,N,G为顶点的三角形与△AOC相似?如果存在,请求出点G的坐标;如果不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com