
科目: 来源: 题型:
【题目】在直角三角形![]() 中,
中,![]() ,
,![]() 平分
平分![]() 交
交![]() 于点
于点![]() ,
,![]() 平分
平分![]() 交
交![]() 于点
于点![]() ,
,![]() 、
、![]() 相交于点
相交于点![]() ,过点
,过点![]() 作
作![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() .下列结论:①
.下列结论:①![]() ;②
;②![]() ;③
;③![]() 平分
平分![]() ;④
;④![]() .其中正确的个数是( )
.其中正确的个数是( )

A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目: 来源: 题型:
【题目】对于二次函数 y ax2 2a 1x a 1a 0,有下列结论:①其图象与 x 轴一定相交;②若 a 0 , 函数在 x 1 时,y 随 x 的增大而减小;③无论 a 取何值,抛物线的顶点始终在同一条直线上;④无论 a 取何值,函数图象都经过同一个点.其中所有正确的结论是:( )
A. ①②③ B. ①③④ C. ①②④ D. ①②③④
查看答案和解析>>
科目: 来源: 题型:
【题目】某市为创建生态文明建设城市,对公路旁的绿化带进行全面改造.现有甲、乙两个工程队,甲队单独完成这项工程,刚好如期完成,每施工一天,需付工程款1.5万元;乙工程队单独完成这项工程要比规定工期多用a天,乙工程队每施工一天需付工程款1万元.若先由甲、乙两队一起合作b天,剩下的工程由乙队单独做,也正好如期完工
(1)当a=6,b=4时,求工程预定工期的天数.
(2)若a﹣b=2.a是偶数
①求甲队、乙队单独完成工期的天数(用含a的代数式表示)
②工程领导小组有三种施工方案:
方案一:甲队单独完成这项工程;
方案二:乙队单独完成这项工程;
方案三:先由甲、乙两队一起合作b天,剩下的工程由乙队单独做.
为了节省工程款,同时又能如期完工,请你选择一种方案,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
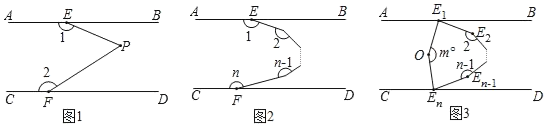
【题目】(提出问题)(1)如图1,已知AB∥CD,证明:∠1+∠EPF+∠2=360°;
(类比探究)(2)如图2,已知AB∥CD,设从E点出发的(n﹣1)条折线形成的n个角分别为∠1,∠2……∠n,探索∠1+∠2+∠3+……+∠n的度数可能在1700°至2000°之间吗?若有可能请求出n的值,若不可能请说明理由.
(拓展延伸)(3)如图3,已知AB∥CD,∠AE1E2的角平分线E1O与∠CEnEn﹣1的角平分线EnO交于点O,若∠E1OEn=m°.求∠2+∠3+∠4+…+∠(n﹣1)的度数.(用含m、n的代数式表示)
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读下面材料:
小明遇到这样一个问题:如图1,在△ABC中,DE∥BC分别交AB于D,交AC于E.已知CD⊥BE,CD=3,BE=4,求BC+DE的值.
小明发现,过点E作EF∥DC,交BC延长线于点F,构造△BEF,经过推理和计算能够使问题得到解决(如图2).

(1)请按照上述思路完成小明遇到的这个问题
(2)参考小明思考问题的方法,解决问题:
如图3,已知ABCD和矩形ABEF,AC与DF交于点G,AC=BF=DF,求∠DGC的度数.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.

(1)求证:AF=DC;
(2)若AB⊥AC,试判断四边形ADCF的形状,并证明你的结论.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,对于直线MN同侧的两个点A,B,若直线MN上的点P满足∠APM=∠BPN,则称点P为A,B在直线MN上的反射点.已知如图2,MN∥HG,AP∥BQ,点P为A,B在直线MN上的反射点,判断点B是否为P,Q在直线HG上的反射点,如果是请证明,如果不是,请说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,将矩形ABCD沿对角线AC剪开,再把△ACD沿CA方向平移得到△A1C1D1,连结AD1、BC1.已知∠ACB=30°,AB=1,
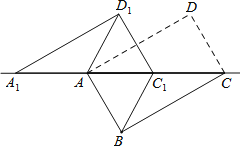
(1)求证:△A1AD1≌△CC1B;
(2)当CC1=1时,求证:四边形ABC1D1是菱形。
查看答案和解析>>
科目: 来源: 题型:
【题目】四张质地相同的卡片如图所示.将卡片洗匀后,背面朝上放置在桌面上.

(1)求随机抽取一张卡片,恰好得到数字2的概率;
(2)小贝和小晶想用以上四张卡片做游戏,游戏规则见信息图.你认为这个游戏公平吗?请用列表法或画树形图法说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某校为加强学生的安全意识,每周通过安全教育APP软件,向家长和学生推送安全教育作业.在最近一期的防溺水安全知识竞赛中,从中抽取了部分学生成绩进行统计.绘制了图中两幅不完整的统计图.请回答如下问题:

(1)m= ,a= ;
(2)补全频数直方图;
(3)该校共有1600名学生.若认定成绩在60分及以下(含60分)的学生安全意识不强,有待进一步加强安全教育,请估计该校安全意识不强的学生约有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com