
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,点![]() ,
,![]() ,边
,边![]() 上有一点
上有一点![]() ,点
,点![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() 上,联结
上,联结![]() ,
,![]() ,联结
,联结![]() ,
,![]() ,
,![]() .
.
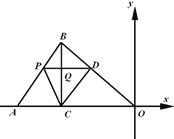
(1)求直线![]() 的解析式及点
的解析式及点![]() 的坐标;
的坐标;
(2当![]() 时,求出点
时,求出点![]() 的坐标;
的坐标;
(3)在(2)的条件下,点![]() 在射线
在射线![]() 上,
上,![]() ,请直接写出点
,请直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】下列调查中,适宜采用全面调查(普查)方式的是( )
A. 对我市市民实施低碳生活情况的调查
B. 对我国首架大型民用飞机零部件的检查
C. 对全国中学生心理健康现状的调查
D. 对市场上的冰淇淋质量的调查
查看答案和解析>>
科目: 来源: 题型:
【题目】某公交车每天的支出费用为60 元,每天的乘车人数 x(人)与每天利润(利润 =票款收入 -支出费用)y(元)的变化关系如下表所示(每位乘客的乘车票价固定不变):
x(人) | … | 200 | 250 | 300 | 350 | 400 | … |
y(元) | … | -20 | -10 | 0 | 10 | 20 | … |
根据表格中的数据,回答下列问题:
(1)在这个变化关系中,自变量是什么?因变量是什么?
(2)若要不亏本,该公交车每天乘客人数至少达到多少?
(3)请你判断一天乘客人数为 5 00人时,利润是多少?
(4) 试写出该公交车每天利润 y(元)与每天乘车人数x (人)的关系式.
查看答案和解析>>
科目: 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为x=1,给出下列结论:
①abc>0;②b2=4ac; ③4a+2b+c>0;④3a+c>0,

其中,正确的结论是______.(写出正确结论的序号)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠BAC=60°.在△ABC的外侧作直线AP,点C关于直线AP的对称点为D,连接AD,BD.
(1)依据题意补全图形;
(2)当∠PAC等于多少度时,AD∥BC?请说明理由;
(3)若BD交直线AP于点E,连接CE,求∠CED的度数;
(4)探索:线段CE,AE和BE之间的数量关系,并说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】已知:二次函数y=x2+bx+c的图象与x轴交于A,B两点,其中A点坐标为(﹣3,0),与y轴交于点C,点D(﹣2,﹣3)在抛物线上.
(1)求抛物线的解析式;
(2)抛物线的对称轴上有一动点P,求出PA+PD的最小值;
(3)点G抛物线上的动点,在x轴上是否存在点E,使B、D、E、G这样的四个点为顶点的四边形是平行四边形?如果存在,求出所有满足条件的E点坐标;如果不存在,请说明理由.

查看答案和解析>>
科目: 来源: 题型:
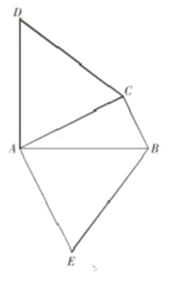
【题目】如图,在△ABC中,DA⊥AB,AD=AB,EA⊥AC,AE=AC.
(1)试说明△ACD≌△AEB;
(2)若∠ACB=90°,连接CE,
①说明EC平分∠ACB;
②判断DC与EB的位置关系,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】关于x的一元二次方程m2x2+(2m﹣1)x+1=0有两个不相等的根a,b,
(1)求实数m的取值范围;
(2)是否存在实数m,使方程的两个实数根互为相反数?如果存在求出m的值,如果不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】水果市场的甲、乙两家商店中都有批发某种水果,批发该种水果x千克时,在甲、乙两家商店所花的钱分别为y1元和y2元,已知y1、y2关于x的函数图象分别为如图所示的折线OAB和射线OC.

(1)当x的取值为 时,在甲乙两家店所花钱一样多?
(2)当x的取值为 时,在乙店批发比较便宜?
(3)如果批发30千克该水果时,在甲店批发比在乙店批发便宜50元,求射线AB的表达式,并写出定义域.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com