
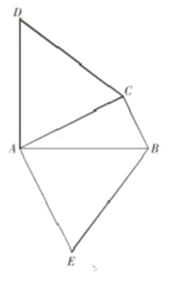
【题目】如图,在△ABC中,DA⊥AB,AD=AB,EA⊥AC,AE=AC.
(1)试说明△ACD≌△AEB;
(2)若∠ACB=90°,连接CE,
①说明EC平分∠ACB;
②判断DC与EB的位置关系,请说明理由.
【答案】(1)详见解析;(2)详见解析;
【解析】
(1)利用垂直证明∠DAC=∠EAB,即可证明全等;
(2)①根据AE=AC,∠ACB=90°,可得∠ACE=∠BCE=45°;
②延长DC交EB于F,先求出∠D=∠ABE,得到∠D+∠BAE+∠AEB=180°,再根据∠D+∠BAD+∠AEB+∠BAE+∠F=360°,求出∠F即可.
(1)∵DA⊥AB,EA⊥AC
∴∠DAB=∠CAE=90°
∴∠DAC+∠CAB=∠BAE+∠CAB
∴∠DAC=∠EAB
∵AD=AB,AE=AC
∴△ACD≌△AEB;
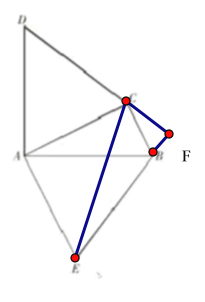
(2)①连接CE,∵DC⊥EB
∵EA⊥AC,AE=AC
∴∠ACE=∠CEA=45°
∵∠ACB=90°
∴∠BCE=45°=∠ACE
∴EC平分∠ACB
②延长DC交EB于F,
∵△ACD≌△AEB
∴∠D=∠ABE
∵∠ABE+∠BAE+∠AEB=180°
∴∠D+∠BAE+∠AEB=180°
∵∠D+∠BAD+∠AEB+∠BAE+∠F=360°
∴∠D+∠BAE+∠AEB+∠BAD+∠F=360°
∴180°+90°+∠F=360°
∴∠F=90°
∴DC⊥EB


科目:初中数学 来源: 题型:
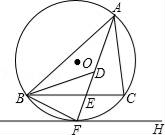
【题目】如图,⊙O是△ABC的外接圆,FH是⊙O的切线,切点为F,FH∥BC,连接AF交BC于E,∠ABC的平分线BD交AF于D,连接BF.
(1)证明:AF平分∠BAC;
(2)证明:BF=FD;
(3)若EF=4,DE=3,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
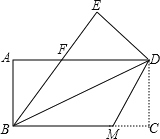
【题目】如图,把一张矩形的纸ABCD沿对角线BD折叠,使点C落在点E处,BE与AD交于点F.
⑴求证:ΔABF≌ΔEDF;
⑵若将折叠的图形恢复原状,点F与BC边上的点M正好重合,连接DM,试判断四边形BMDF的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
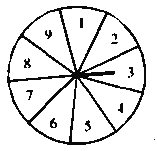
【题目】如图,一个均匀的转盘被平均分成9等份,分别标有1,2,3,4,5,6,7,8,9这9个数字.转动转盘,当转盘停止后,指针指向的数字即为转出的数字.
小亮和小芳两人玩转盘游戏,对游戏规则,小芳提议:若转岀的数字是3的倍数,小芳获胜,若转出的数字是4的倍数,小亮获胜.
(1)你认为小芳的提议合理吗?为什么?
(2)利用这个转盘,请你为他俩设计一种对两人都公平的游戏规则.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,由正比例函数![]() 沿
沿![]() 轴的正方向平移4个单位而成的一次函数
轴的正方向平移4个单位而成的一次函数![]()
的图像与反比例函数![]() (
(![]() )在第一象限的图像交于A(1,n)和B两点.
)在第一象限的图像交于A(1,n)和B两点.
(1)求一次函数![]() 和反比例函数的解析式;
和反比例函数的解析式;
(2)求△ABO的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公交车每天的支出费用为60 元,每天的乘车人数 x(人)与每天利润(利润 =票款收入 -支出费用)y(元)的变化关系如下表所示(每位乘客的乘车票价固定不变):
x(人) | … | 200 | 250 | 300 | 350 | 400 | … |
y(元) | … | -20 | -10 | 0 | 10 | 20 | … |
根据表格中的数据,回答下列问题:
(1)在这个变化关系中,自变量是什么?因变量是什么?
(2)若要不亏本,该公交车每天乘客人数至少达到多少?
(3)请你判断一天乘客人数为 5 00人时,利润是多少?
(4) 试写出该公交车每天利润 y(元)与每天乘车人数x (人)的关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解同学对体育活动的喜爱情况,某校设计了“你最喜欢的体育活动是哪一项(仅限一项)”的调查问卷该校对本校学生进行随机抽样调查,以下是根据调查数据得到的统计图的部分。
抽样调查学生最喜欢的体育活动人数的直方图 抽样调查学生最喜欢的体育活动人数扇形统计图.

请根据以上信息解答以下问题:
(1)该校对多少名学生进行了抽样调查?
(2)①请补全图1并标上数据,②图2中![]() =________;
=________;
(3)若该校共有学生800人,请你估计该校最喜羽毛球项目的学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校举行“汉字听写”比赛,每位学生听写汉字![]() 个,比赛结束后随机抽查部分学生的听写结果,以下是根据抽查结果绘制的统计图的一部分.
个,比赛结束后随机抽查部分学生的听写结果,以下是根据抽查结果绘制的统计图的一部分.
组别 | 正确字数 | 人数 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

根据以上信息解决下列问题:
(1)在统计表中,![]() __________,
__________,![]() __________,并补全直方图;
__________,并补全直方图;
(2)扇形统计图中“![]() 组”所对应的圆心角的度数是__________度;
组”所对应的圆心角的度数是__________度;
(3)若该校共有![]() 名学生,如果听写正确的个数少于
名学生,如果听写正确的个数少于![]() 个定为不合格,请你估计这所学校本次比赛听写不合格的学生人数.
个定为不合格,请你估计这所学校本次比赛听写不合格的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:

小亮遇到这样问题:如图1,已知AB∥CD,EOF是直线AB、CD间的一条折线.判断∠O、∠BEO、∠DFO三个角之间的数量关系.小亮通过思考发现:过点O作OP∥AB,通过构造内错角,可使问题得到解决.
请回答:∠O、∠BEO、∠DFO三个角之间的数量关系是 .
参考小亮思考问题的方法,解决问题:
(2)如图2,将△ABC沿BA方向平移到△DEF(B、D、E共线),∠B=50°,AC与DF相交于点G,GP、EP分别平分∠CGF、∠DEF相交于点P,求∠P的度数;
(3)如图3,直线m∥n,点B、F在直线m上,点E、C在直线n上,连接FE并延长至点A,连接BA、BC和CA,做∠CBF和∠CEF的平分线交于点M,若∠ADC=α,则∠M= (直接用含α的式子表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com