
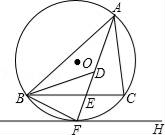
【题目】如图,⊙O是△ABC的外接圆,FH是⊙O的切线,切点为F,FH∥BC,连接AF交BC于E,∠ABC的平分线BD交AF于D,连接BF.
(1)证明:AF平分∠BAC;
(2)证明:BF=FD;
(3)若EF=4,DE=3,求AD的长.
【答案】(1)证明见解析;(2)证明见解析;(3)![]() .
.
【解析】试题分析:(1)连接OF,通过切线的性质证OF⊥FH,进而由FH∥BC,得OF⊥BC,即可由垂径定理得到F是弧BC的中点,根据圆周角定理可得∠BAF=∠CAF,由此得证;
(2)求BF=FD,可证两边的对角相等;易知∠DBF=∠DBC+∠FBC,∠BDF=∠BAD+∠ABD;观察上述两个式子,∠ABD、∠CBD是被角平分线平分∠ABC所得的两个等角,而∠CBF和∠DAB所对的是等弧,由此可证得∠DBF=∠BDF,即可得证;
(3)由EF、DE的长可得出DF的长,进而可由(2)的结论得到BF的长;然后证△FBE∽△FAB,根据相似三角形得到的成比例线段,可求出AF的长,即可由AD=AF-DF求出AD的长.
试题解析:(1)证明:连接OF
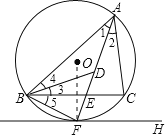
∵FH是⊙O的切线
∴OF⊥FH
∵FH∥BC,
∴OF垂直平分BC
∴![]() ,
,
∴∠1=∠2,
∴AF平分∠BAC
(2)证明:由(1)及题设条件可知
∠1=∠2,∠4=∠3,∠5=∠2
∴∠1+∠4=∠2+∠3
∴∠1+∠4=∠5+∠3
∵∠1+∠4=∠BDF,∠5+∠3=∠FBD,
∴∠BDF=∠FBD,
∴BF=FD(6分)
(3)解:在△BFE和△AFB中
∵∠5=∠2=∠1,∠AFB=∠AFB,
∴△BFE∽△AFB
∴![]() ,
,
∴BF2=FEFA
∴![]() ,EF=4,BF=FD=EF+DE=4+3=7,
,EF=4,BF=FD=EF+DE=4+3=7,
∴![]()
∴AD=AF-DF=AF-(DE+EF)=![]() .
.
考点: 1.切线的性质;2.角平分线的性质;3.垂径定理;4.相似三角形的判定与性质.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】(1)(操作发现)
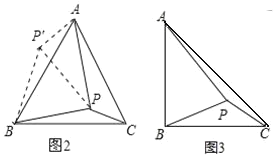
如图 1,在边长为 1 个单位长度的小正方形组成的网格中,ABC 的三个顶点均在格点上.现将ABC 绕点 A 按顺时针方向旋转 90°,点 B 的对应点为 B′,点 C 的对应点为 C′, 连接 BB′,如图所示则∠AB′B= .
(2)(解决问题)
如图 2,在等边ABC 内有一点 P,且 PA=2,PB=![]() ,PC=1,如果将△BPC 绕点 B 顺时针旋转 60°得出△ABP′,求∠BPC 的度数和 PP′的长;
,PC=1,如果将△BPC 绕点 B 顺时针旋转 60°得出△ABP′,求∠BPC 的度数和 PP′的长;
(3)(灵活运用)
如图 3,将(2)题中“在等边ABC 内有一点 P 改为“在等腰直角三角形 ABC 内有一点P”,且 BA=BC,PA=6,BP=4,PC=2,求∠BPC 的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列四项调查中,方式正确的是![]()
![]()
A. 了解本市中学生每天学习所用的时间,采用全面调查的方式
B. 为保证运载火箭的成功发射,对其所有的零部件采用抽样调查的方式
C. 了解某市每天的流动人口数,采用全面调查的方式
D. 了解全市中学生的视力情况,采用抽样调查的方式
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校七(1)班学生为了解某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理,已知该小区用水量不超过![]() 的家庭占被调查家庭总数的百分比为12%,请根据以上信息解答下列问题:
的家庭占被调查家庭总数的百分比为12%,请根据以上信息解答下列问题:
级别 |
|
|
|
|
|
|
月均用水量 |
|
|
|
|
|
|
频数(户) | 6 | 12 |
| 10 | 4 | 2 |
(1)本次调查采用的方式是 (填“普查”或“抽样调查”),样本容量是 ;
(2)补全频率分布直方图;

(3)若将调查数据绘制成扇形统计图,则月均用水量“![]() ”的圆心角度数是 .
”的圆心角度数是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读理解下面的例题,再按要求解答下列问题: 同学们,我们把学习新的数学知识的时候,经常利用“化归“的数学思想方法解决问题,比如,我们在学习二元一次方程组的解法时,是通过“消元”的方法将二元方程化归成我们所 熟悉的一元方程,从而正确求解.下面我们就利用“化归”的数学方法解决新的问题. 首先,我们把像这样,只含有一个未知数,并且未知教的最高次数是![]() 的不等式,称为一元二次不等式.通过以前的学习,我们已经认识了一无一次不等式、一元一次不等式组并掌握 了它们的解法.同学们,你们能类比一元一次不等式(组)的解法求出一元二次不等式的解 集吗? 例题:解一元二次不等式
的不等式,称为一元二次不等式.通过以前的学习,我们已经认识了一无一次不等式、一元一次不等式组并掌握 了它们的解法.同学们,你们能类比一元一次不等式(组)的解法求出一元二次不等式的解 集吗? 例题:解一元二次不等式![]() 为了解决这个问题,我们需要将一元二次不等式“化归”到一元一次不等式(组),通过平方差公式的逆用,我们可以把
为了解决这个问题,我们需要将一元二次不等式“化归”到一元一次不等式(组),通过平方差公式的逆用,我们可以把![]() 写成
写成![]() 的形式,从面将
的形式,从面将![]() 转化为
转化为![]() ,然后再利用两数相乘的符号性质将一元二次不等式转化成一元一次不等式(组),从而解决问题.
,然后再利用两数相乘的符号性质将一元二次不等式转化成一元一次不等式(组),从而解决问题.
解:![]()
![]() 可化为
可化为![]()
由有理数的乘法法则“两数相乘,同号得正”,得①![]() ②
②![]()
解不等式组①, ![]()
解不等式组②, ![]()
即一元二次不等式![]() 的解集为
的解集为![]()
拓展应用:
![]() 求一元二次不等式
求一元二次不等式![]() 的解集.
的解集.
![]() 求分式不等式
求分式不等式![]() 的解集.
的解集.
![]() 求一元二次不等式
求一元二次不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为解决中小学大班额问题,某县今年将改扩建部分中小学,根据预算,改扩建3所中学和2所小学共需资金6200万元,改扩建1所中学和3所小学共需资金4400万元
(1)改扩建1所中学和1所小学所需资金分别是多少万元?
(2)该县计划改扩建中小学共10所,改扩建资金由国家财政和地方财政共同承担.若国家财政拨付资金不超过8400万元;地方财政投入资金不少于4000万元,其中地方财政投入到中小学的改扩建资金分别为每所500万元和300万元,请问共有哪几种改扩建方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
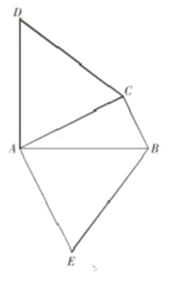
【题目】如图,在△ABC中,DA⊥AB,AD=AB,EA⊥AC,AE=AC.
(1)试说明△ACD≌△AEB;
(2)若∠ACB=90°,连接CE,
①说明EC平分∠ACB;
②判断DC与EB的位置关系,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com