第二步：构造一个长为x，宽为（x﹣2）的长方形，长比宽大2，且面积为3，如图所示．

第三步：用四个这样的长方形围成一个大正方形，中间是一个小正方形，如图所示．

第四步：计算大正方形面积用x表示为　　 　　．长方形面积为常数　　 ．小正方形面积为常数　　 ．

由观察可得，大正方形面积等于四个长方形与小正方形面积之和，得方程　　 　，两边开方可求得：x1=3，x2=﹣1．

（1）第四步中横线上应填入　　 　　；　　 　　；　　 　　；　　 　　．

（2）请参考古人的思考过程，画出示意图，写出步骤，解方程x2﹣x﹣1=0．

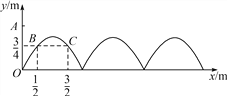
【题目】如图，需在一面墙上绘制几个相同的抛物线型图案．按照图中的直角坐标系，最左边的抛物线可以用y＝ax2＋bx(a≠0)表示．已知抛物线上B，C两点到地面的距离均为m，到墙边OA的距离分别为m，m.

(1)求该拋物线的函数关系式，并求图案最高点到地面的距离；

(2)若该墙的长度为10 m，则最多可以连续绘制几个这样的拋物线型图案？

【题目】如图，在ABCD中，对角线AC、BD相交于点O，点E、F分别是边AD、AB上的点，连结OE、OF、EF．若AB=7，BC=5，∠DAB=45°，则①点C到直线AB的距离是_____.②△OEF周长的最小值是________．

(1)求b的值；

(2)若A(－2，y1)，B(5，y2)是抛物线y＝2x2＋bx＋1上的两点，试比较y1与y2的大小关系；

(3)将抛物线y＝2x2＋bx＋1的图象向上平移k(k是正整数)个单位长度，使平移后的图象与x轴无交点，求k的最小值．

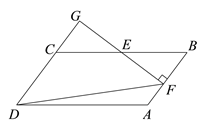
（1）求证：GD=GF.

（2）已知BC=10， .求 CD的长.

（1）若∠B=35°，∠ACB=85°，求∠E得度数．

（2）当点P在线段AD上运动时，设∠B=α，∠ACB=β（β＞α），求∠E得大小．（用含α、β的代数式表示）

①若a+b+c=0，则b2﹣4ac＞0；

②若方程两根为﹣1和2，则2a+c=0；

③若方程ax2+c=0有两个不相等的实根，则方程ax2+bx+c=0必有两个不相等的实根；

④若b=2a+c，则方程有两个不相等的实根．其中正确的有（　　）

A. ①②③ B. ①②④ C. ②③④ D. ①②③④

【题目】（1）①如图1，已知，，可得__________.

②如图2，在①的条件下，如果平分，则__________.

③如图3，在①、②的条件下，如果，则__________.

（2）尝试解决下面问题：已知如图4，，，是的平分线，，求的度数.