
【题目】在ABCD中,AE平分∠BAD交边BC于E,DF⊥AE,交边BC于F,若AD=10,EF=4,则AB=_____.
【答案】7或3
【解析】
分AE与DF的交点在矩形内和矩形外两个情况讨论,利用勾股定理可求的AB的值.
解:①如图: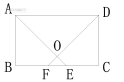
当AE与DF的交点为O点,当O在矩形内时,
在□ABCD中,由AE平分∠BAD交边BC于E,DF⊥AE,
易得:△ABE、△AOD、△OEF均为等要直角三角形,
在RT△ABE中,设AB=x,可得AE=![]() =
=![]() x,
x,
在RT△OEF中由EF=4,可得OE=![]() ,
,
![]() AO=AE-OE=
AO=AE-OE=![]() x-
x-![]() ,
,
在RT△AOD中,可得AD=![]() AO,
AO,
即:10=![]()
![]() (
(![]() x-
x-![]() ),10=2x-4,x=7;
),10=2x-4,x=7;
②如图: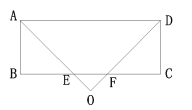
同理可得,设AB=x,AE=![]() =
=![]() x,OE=
x,OE=![]()
![]() AO=AE+OE=
AO=AE+OE=![]() x+
x+![]() ,AD=
,AD=![]() AO,
AO,
可得:10=![]()
![]() (
(![]() x+
x+![]() ),10=2x+4,x=3;
),10=2x+4,x=3;
综合所述:x=7或x=3;
故答案:7或3.


科目:初中数学 来源: 题型:
【题目】如图,矩形OABC的顶点A,B的坐标分别为(4,0),(4,3),动点M,N分别从O,B同时出发.以每秒1个单位的速度运动.其中,点M沿OA向终点A运动,点N沿BC向终点C运动.过点M作MP⊥OA,交AC于P,连接NP,已知动点运动了![]() 秒.
秒.
(1)当![]() 时,求PC的长;
时,求PC的长;
(2)当![]() 为何值时,△NPC是以PC为腰的等腰三角形?
为何值时,△NPC是以PC为腰的等腰三角形?
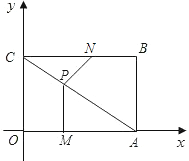
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售A,B两种品牌的多媒体教学设备,这两种多媒体教学设备的进价和售价如表所示.

(1)若该商场计划购进两种多媒体教学设备若干套,共需124万元,全部销售后可获毛利润36万元.则该商场计划购进A,B两种品牌的多媒体教学设备各多少套?
(2)通过市场调研,该商场决定在(1)中所购总数量不变的基础上,减少A种设备的购进数量,增加B种设备的购进数量.若用于购进这两种多媒体教学设备的总资金不超过120万元,且全部销售后可获毛利润不少于33.6万元.问有几种购买方案?并写出购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“赏中华诗词,寻文化基因,品生活之美”,某校举办了首届“中国诗词大会”,经选拔后有50名学生参加决赛,这50名学生同时默写50首古诗词,若每正确默写出一首古诗词得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
组别 | 成绩x分 | 频数 |
第1组 |
| 6 |
第2组 |
| 8 |
第3组 |
| 14 |
第4组 |
| a |
第5组 |
| 10 |
请结合图表完成下列各题:
![]() 求表中a的值;
求表中a的值; ![]() 频数分布直方图补充完整;
频数分布直方图补充完整;
![]() 若测试成绩不低于80分为优秀,则本次测试的优秀率是多少?
若测试成绩不低于80分为优秀,则本次测试的优秀率是多少?
![]() 第5组10名同学中,有4名男同学,现将这10名同学平均分成两组进行对抗练习,且4名男同学每组分两人,求小明与小强两名男同学能分在同一组的概率.
第5组10名同学中,有4名男同学,现将这10名同学平均分成两组进行对抗练习,且4名男同学每组分两人,求小明与小强两名男同学能分在同一组的概率.
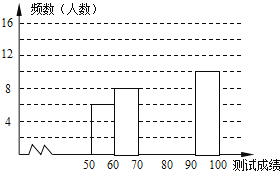
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把正整数1,2,3,4,…排列成如图所示的一个表.
(1)用一正方形在表中随意框住4个数,把其中最大的数记为x,另三个数用含x的式子表示出来,从大到小依次是 , , ;
(2)在(1)的前提下,当被框住的4个数之和等于984时,x位于该表的第几行第几列?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点A(0,2),△AOB为等边三角形,P是x轴上一个动点(不与原点O重合),以线段AP为一边在其右侧作等边三角形APQ.
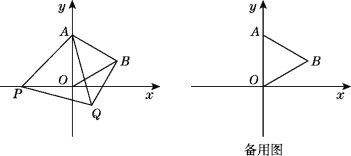
(1)求点B的坐标.
(2)在点P运动过程中,∠ABQ的大小是否发生改变?若不改变,求出其大小;若改变,请说明理由.
(3)连接OQ,当OQ∥AB时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F.

(1)CD与EF平行吗?为什么?
(2)如果∠1=∠2,且∠3=120°,求∠ACB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了奖励学习进步的同学,某班准备购买甲、乙、丙三种不同的笔记本作为奖品,其单价分别为2元、3元、4元,购买这些笔记本需要花60元;经过协商,每种笔记本单价下降0.5元,只花了49元,那么以下哪个结论是正确的( )
A. 乙种笔记本比甲种笔记本少4本
B. 甲种笔记本比丙种笔记本多6本
C. 乙种笔记本比丙种笔记本多8本
D. 甲种笔记本与乙种笔记本共12本
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com