
科目: 来源: 题型:
【题目】自主学习,请阅读下列解题过程.
解一元二次不等式:x2﹣5x>0.
解:设x2﹣5x=0,解得:x1=0,x2=5,则抛物线y=x2﹣5x与x轴的交点坐标为(0,0)和(5,0).画出二次函数y=x2﹣5x的大致图象(如图所示),由图象可知:当x<0,或x>5时函数图象位于x轴上方,此时y>0,即x2﹣5x>0,所以,一元二次不等式x2﹣5x>0的解集为:x<0,或x>5.
通过对上述解题过程的学习,按其解题的思路和方法解答下列问题:
(1)上述解题过程中,渗透了下列数学思想中的 和 .(只填序号)
①转化思想 ②分类讨论思想 ③数形结合思想
(2)一元二次不等式x2﹣5x<0的解集为 .
(3)用类似的方法解一元二次不等式:x2﹣2x﹣3>0.
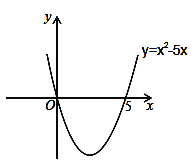
查看答案和解析>>
科目: 来源: 题型:
【题目】下列说法中:①0是最小的整数;②有理数不是正数就是负数;③正整数、负整数、正分数、负分数统称为有理数;④非负数就是正数;④![]() 不仅是有理数,而且是分数;⑤
不仅是有理数,而且是分数;⑤![]() 是无限不循环小数,所以不是有理数;⑥无限小数不都是有理数;⑦正数中没有最小的数,负数中没有最大的数.其中错误的说法的个数为( )
是无限不循环小数,所以不是有理数;⑥无限小数不都是有理数;⑦正数中没有最小的数,负数中没有最大的数.其中错误的说法的个数为( )
A. 7个B. 6个C. 5个D. 4个
查看答案和解析>>
科目: 来源: 题型:
【题目】已知有理数a、b、c在数轴上的位置如图所示,且|a|=|b|,则下列结论中错误的是( )
![]()
A. a+c<0B. -a+b+c<0
C. |a+b|>|a+c|D. |a+b|<|a+c|
查看答案和解析>>
科目: 来源: 题型:
【题目】几年前我国曾经流行有一种叫“二十四点”的数学趣味算题,方法是给出1~13之间的自然数,从中任取四个,将这四个数(四个数都只能用一次)进行“+”“-”“×”“÷”运算,可加括号使其结果等于24.
例如:对1,2,3,4可运算(1+2+3)×4=24,也可以写成4×(1+2+3)=24,但视作相同的方法.
现有郑、付两同学的手中分别握着四张扑克牌(见下图);若红桃、方块上的点数记为负数,黑桃、梅花上的点数记为正数.
请你对郑、付两同学的扑克牌的按要求进行记数,并按前面“二十四点”运算方式对郑、付两同学的记数分别进行列式计算,使其运算结果均为24.(分别尽可能提供多种算法)

依次记为:______ 、______ 、______ 、______

依次记为:______ 、______ 、______ 、______ .
(1)帮助郑同学列式计算:______
(2)帮助付同学列式计算:______ .
查看答案和解析>>
科目: 来源: 题型:
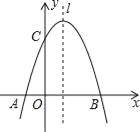
【题目】如图,已知抛物线y=![]() +mx+3与x轴交于A,B两点,与y轴交于点C,点B的坐标为(3,0),
+mx+3与x轴交于A,B两点,与y轴交于点C,点B的坐标为(3,0),
(1)求m的值及抛物线的顶点坐标.
(2)点P是抛物线对称轴l上的一个动点,当PA+PC的值最小时,求点P的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,二次函数y=(x+2)2+m的图象与y轴交于点C,点B在抛物线上,且与点C关于抛物线的对称轴对称,已知一次函数y=kx+b的图象经过该二次函数图象上的点A(﹣1,0)及点B.
(1)求二次函数与一次函数的解析式;
(2)根据图象,写出满足(x+2)2+m≥kx+b的x的取值范围.

查看答案和解析>>
科目: 来源: 题型:
【题目】某巡警骑摩托车在一条南北大道上巡逻,某天他从岗亭出发,晚上停留在A处,规定向北方向为正,当天行驶纪录如下(单位:千米)+10,-9,+7,-15,+6,-14,+4,-2
(1)A在岗亭何方?距岗亭多远?
(2)若摩托车行驶1千米耗油0.05升,这一天共耗油多少升?
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读材料:求1+2+22+23+24+…+22019的值.
解:设S=1+2+22+23+24+…+22019,将等式两边同时乘以2得:2S=2+22+23+24+25+…+22019+22020
将下式减去上式得2S-S=22020-1
即S=22020-1
即1+2+22+23+24+…=22020-1
请你仿照此法计算:
(1)1+2+22+23+24+…+220
(2)1+5+52+53+54+…+5n(其中n为正整数).
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在数轴上,点A表示1,现将点A沿数轴做如下移动:第一次将点A向左移动3个单位长度到达点A1,第2次将点A1向右平移6个单位长度到达点A2,第3次将点A2向左移动9个单位长度到达点A3…则第6次移动到点A6时,点A6在数轴上对应的实数是_____;按照这种规律移动下去,第2019次移动到点A2019时,A2019在数轴上对应的实数是_____.
![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】某网店销售某款童装,每件售价60元,每星期可卖300件,为了促销,该网店决定降价销售.市场调查反映:每降价1元,每星期可多卖30件.已知该款童装每件成本价40元,设该款童装每件售价x元,每星期的销售量为y件.
(1)求y与x之间的函数关系式;
(2)当每件售价定为多少元时,每星期的销售利润最大,最大利润多少元?
(3)若该网店每星期想要获得不低于6480元的利润,每星期至少要销售该款童装多少件?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com