
科目: 来源: 题型:
【题目】甲、乙二人在圆形跑道上从同一点A同时出发,并按相反方向跑步,甲的速度为每秒5m,乙的速度为每秒8m,到他们第一次在A点处再度相遇时跑步就结束.则从他们开始出发(算第一次相遇)到结束(算最后一次相遇)共相遇了__________ 次.
查看答案和解析>>
科目: 来源: 题型:
【题目】某旅行社推出一条成本价为500元/人的省内旅游线路.游客人数![]() (人/月)与旅游报价
(人/月)与旅游报价![]() (元/人)之间的关系为
(元/人)之间的关系为![]() ,已知:旅游主管部门规定该旅游线路报价在800元/人~1200元/人之间.
,已知:旅游主管部门规定该旅游线路报价在800元/人~1200元/人之间.
(1)要将该旅游线路每月游客人数控制在200人以内,求该旅游线路报价的取值范围;
(2)求经营这条旅游线路每月所需要的最低成本;
(3)当这条旅游线路的旅游报价为多少时,可获得最大利润?最大利润是多少?
查看答案和解析>>
科目: 来源: 题型:
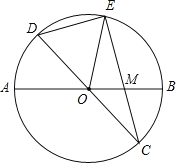
【题目】已知:如图,在半径为4的⊙O中,AB、CD是两条直径,M为OB的中点,CM的延长线交⊙O于点E,且EM>MC.连接DE,DE=![]() .
.
(1)求证:AMMB=EMMC;
(2)求EM的长;
(3)求sin∠EOB的值.
【答案】(1)证明见解析(2)4(3)![]()
【解析】(1)连接A、C,E、B点,那么只需要求出△AMC和△EMB相似,即可求出结论,根据圆周角定理可推出它们的对应角相等,即可得△AMC∽△EMB;
(2)根据圆周角定理,结合勾股定理,可以推出EC的长度,根据已知条件推出AM、BM的长度,然后结合(1)的结论,很容易就可求出EM的长度;
(3)过点E作EF⊥AB,垂足为点F,通过作辅助线,解直角三角形,结合已知条件和(1)(2)所求的值,可推出Rt△EOF各边的长度,根据锐角三角函数的定义,便可求得sin∠EOB的值.
【题型】解答题
【结束】
21
【题目】为大力弘扬“奉献、友爱、互助、进步”的志愿服务精神,传播“奉献他人、提升自我”的志愿服务理念,合肥市某中学利用周末时间开展了“助老助残、社区服务、生态环保、网络文明”四个志愿服务活动(每人只参加一个活动),九年级某班全班同学都参加了志愿服务,班长为了解志愿服务的情况,收集整理数据后,绘制以下不完整的统计图,请你根据统计图中所提供的信息解答下列问题:
(1)请把折线统计图补充完整;
(2)求扇形统计图中,网络文明部分对应的圆心角的度数;
(3)小明和小丽参加了志愿服务活动,请用树状图或列表法求出他们参加同一服务活动的概率.

查看答案和解析>>
科目: 来源: 题型:
【题目】某水果店用500元购进甲、乙两种水果共50kg,这两种水果的进价、售价如下表所示
品名 | 甲种 | 乙种 |
进价 | 7 | 12 |
售价 | 10 | 16 |
![]() 求这两种水果各购进多少千克?
求这两种水果各购进多少千克?
![]() 如果这批水果当天售完,水果店除进货成本外,还需其它成本
如果这批水果当天售完,水果店除进货成本外,还需其它成本![]() 元
元![]() ,那么水果店销售完这批水果获得的利润是多少元?(利润
,那么水果店销售完这批水果获得的利润是多少元?(利润![]() 售价
售价![]() 成本)
成本)
查看答案和解析>>
科目: 来源: 题型:
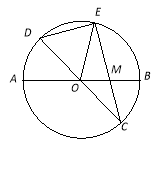
【题目】已知:如图,在半径为4的⊙O中,AB、CD是两条直径,M为OB的中点,CM的延长线交⊙O于点E,且EM>MC.连结DE,DE=![]() .
.
(1)求证:![]() ;
;
(2)求EM的长;
(3)求sin∠EOB的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】观察下面的点阵图和相应的等式,探究其中的规律:
(1)认真观察,并在④后面的横线上写出相应的等式.
![]()
①1=1 ②1+2=![]() =3 ③1+2+3=
=3 ③1+2+3=![]() =6 ④ …
=6 ④ …
(2)结合(1)观察下列点阵图,并在⑤后面的横线上写出相应的等式.
![]()
1=12②1+3=22③3+6=32④6+10=42⑤ …
(3)通过猜想,写出(2)中与第n个点阵相对应的等式 .
【答案】(1)10;(2)见解析;(3)![]()
【解析】试题分析:(1)根据①②③观察会发现第四个式子的等号的左边是1+2+3+4,右边分子上是(1+4)×4,从而得到规律;
(2)通过观察发现左边是10+15,右边是25即5的平方;
(3)过对一些特殊式子进行整理、变形、观察、比较,归纳出一般规律.
试题解析:(1)根据题中所给出的规律可知:1+2+3+4=![]() =10;
=10;
(2)由图示可知点的总数是5×5=25,所以10+15=52.
(3)由(1)(2)可知![]()
点睛:主要考查了学生通过特例分析从而归纳总结出一般结论的能力.对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的.通过分析找到各部分的变化规律后用一个统一的式子表示出变化规律是此类题目中的难点.
【题型】解答题
【结束】
19
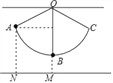
【题目】如图,用细线悬挂一个小球,小球在竖直平面内的A、C两点间来回摆动,A点与地面距离AN=14cm,小球在最低点B时,与地面距离BM=5cm,∠AOB=66°,求细线OB的长度.(参考数据:sin66°≈0.91,cos66°≈0.40,tan66°≈2.25)
查看答案和解析>>
科目: 来源: 题型:
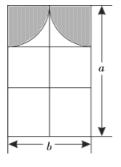
【题目】装修公司给小红家的窗户设计了如图所示的装修方案,上方布料窗眉(阴影部分)由两个半径相同的四分之一圆组成.
(1)分别用整式表示窗眉用布和窗户透光的面积.(窗框的面积忽略不计).
(2)观察(1)中的结果,它们是单项式还是多项式?次数分别是多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知数轴上点A表示的数为6,B是数轴上一点,且AB=10.动点P从点O出发,以每秒6个单位长度的速度沿数轴向右匀速运动,设运动时间为t(t>0)秒.
(1)写出数轴上点B表示的数 ;当t=3时,OP=
(2)动点R从点B出发,以每秒8个单位长度的速度沿数轴向右匀速运动,若点P,R同时出发,问点R运动多少秒时追上点P?
(3)动点R从点B出发,以每秒8个单位长度的速度沿数轴向右匀速运动,若点P,R同时出发,问点R运动多少秒时PR相距2个单位长度?
![]()
查看答案和解析>>
科目: 来源: 题型:
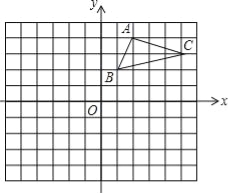
【题目】如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,4),请解答下列问题:
(1)画出△ABC关于x轴对称的△A1B1C1,并写出点A1的坐标.
(2)画出△A1B1C1绕原点O旋转180°后得到的△A2B2C2,并写出点A2的坐标.
【答案】(1)作图见解析;点A1的坐标(2,﹣4);(2)作图见解析;点A2的坐标(﹣2,4).
【解析】
试题分析:(1)分别找出A、B、C三点关于x轴的对称点,再顺次连接,然后根据图形写出A点坐标;
(2)将△A1B1C1中的各点A1、B1、C1绕原点O旋转180°后,得到相应的对应点A2、B2、C2,连接各对应点即得△A2B2C2.
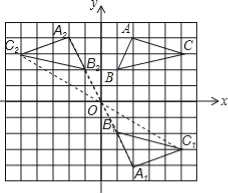
试题解析:(1)如图所示:点A1的坐标(2,﹣4);
(2)如图所示,点A2的坐标(﹣2,4).
考点:1.作图-旋转变换;2.作图-轴对称变换.
【题型】解答题
【结束】
18
【题目】观察下面的点阵图和相应的等式,探究其中的规律:
(1)认真观察,并在④后面的横线上写出相应的等式.
![]()
①1=1 ②1+2=![]() =3 ③1+2+3=
=3 ③1+2+3=![]() =6 ④ …
=6 ④ …
(2)结合(1)观察下列点阵图,并在⑤后面的横线上写出相应的等式.
![]()
1=12②1+3=22③3+6=32④6+10=42⑤ …
(3)通过猜想,写出(2)中与第n个点阵相对应的等式 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com