【题目】如图，正方形网格中小方格边长为1，请你根据所学的知识解决下面问题．

【题目】勾股定理神秘而美妙，它的证法多样，其巧妙各有不同，其中的“面积法”给了小聪以灵感，他惊喜的发现，当两个全等的直角三角形如图1或图2摆放时，都可以用“面积法”来证明，下面是小聪利用图1证明勾股定理的过程：

【题目】如图，在Rt△ABC中，∠ACB=90°，BD是∠ABC的平分线，点O在AB上，⊙O经过B，D两点，交BC于点E．

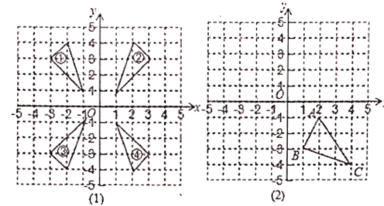
【题目】（1）在图(1)中编号①②③④的四个三角形中，关于y轴对称的两个三角形的编号为_________；关于x轴对称的两个三角形的编号为___________；

【题目】如图，直线OD与x轴所夹的锐角为30°，OA1的长为2，△A1A2B1、△A2A3B2、△A3A4B3…△AnAn+1Bn均为等边三边形，点A1、A2、A3…An﹣1在x轴正半轴上依次排列，点B1、B2、B3…Bn在直线OD上依次排列，那么点B2的坐标为____，点Bn的坐标为____．

【题目】（1）阅读理解：

【题目】如图，AB是⊙O的直径，C，D是⊙O上的点，且OC∥BD，AD分别与BC，OC相交于点E，F，则下列结论：①AD⊥BD；②∠AOC=∠AEC；③CB平分∠ABD；④AF=DF；⑤BD=2OF；⑥△CEF≌△BED，其中一定成立的____（把你认为正确结论的序号都填上）

【题目】如图，在△ABC中，AB边的垂直平分线l1交BC于点D，AC边的垂直平分线l2交BC于点E，l1与l2相交于点O，连结0B，OC.若△ADE的周长为12cm，△OBC的周长为32cm.

【题目】如图，在等腰直角三角形ABC中，∠ABC=90°，D为AC边上的中点，过D点作DE⊥DF，交AB于点E，交BC于点F，若AE=8，FC=6.

【题目】如图，在小山的东侧A点有一个热气球，由于受风的影响，以30米/分的速度沿与地面成75°角的方向飞行，25分钟后到达C处，此时热气球上的人测得小山西侧B点的俯角为30°，则小山东西两侧A，B两点间的距离为（　　）米．