
科目: 来源: 题型:
【题目】如图,某市近郊有一块长为60米,宽为50米的矩形荒地,地方政府准备在此建一个综合性休闲广场,其中阴影部分为通道,通道的宽度均相等,中间的三个矩形(其中三个矩形的一边长均为a米)区域将铺设塑胶地面作为运动场地.设通道的宽度为x米.

(1)a= (用含x的代数式表示);
(2)若塑胶运动场地总占地面积为 2430平方米,则通道的宽度为多少米?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,将三角板放在正方形ABCD上,使三角板的直角顶点E与正方形ABCD的顶点A重合,三角扳的一边交CD于点F.另一边交CB的延长线于点G.
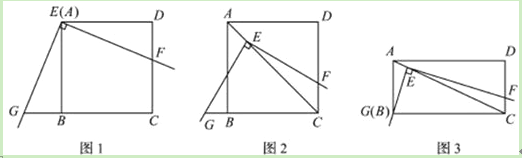
(1)求证:EF=EG;
(2)如图2,移动三角板,使顶点E始终在正方形ABCD的对角线AC上,其他条件不变,(1)中的结论是否仍然成立?若成立,请给予证明:若不成立.请说明理由:
(3)如图3,将(2)中的“正方形ABCD”改为“矩形ABCD”,且使三角板的一边经过点B,其他条件不变,若AB=a、BC=b,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知甲乙两地之间的距离为810米,小明和小天分别从甲乙两地出发,匀速相向而行,已知小明先出发1分钟后,小天再出发,两人在甲乙之间的丙地相遇,此时,小明发现有小学同学也在丙地,于是聊了一会儿,随后以原来速度的![]() 倍返回甲地,小天相遇后继续以原速向甲地前行,到达甲地后立即原速返回,直至再次与小明相遇.已知在整个过程中,小明、小天两人之间的距离
倍返回甲地,小天相遇后继续以原速向甲地前行,到达甲地后立即原速返回,直至再次与小明相遇.已知在整个过程中,小明、小天两人之间的距离![]() (米与小明出发的时间
(米与小明出发的时间![]() (分钟)之间的关系如图所示,则在第二次相遇时两人距离乙地______米.
(分钟)之间的关系如图所示,则在第二次相遇时两人距离乙地______米.
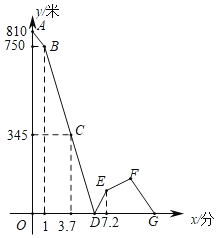
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,![]() 个边长为
个边长为![]() 的相邻正方形的一边均在同一直线上,点
的相邻正方形的一边均在同一直线上,点![]() ,
,![]() ,
,![]() ,…
,…![]() 分别为边
分别为边![]() ,
,![]() ,
,![]() ,…,
,…,![]() 的中点,
的中点,![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() ,…
,…![]() 的面积为
的面积为![]() ,则
,则![]() ________.(用含
________.(用含![]() 的式子表示)
的式子表示)

查看答案和解析>>
科目: 来源: 题型:
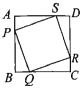
【题目】如图,![]() 四个小球分别从正方形的四个顶点
四个小球分别从正方形的四个顶点![]() 处出发(小球的大小忽略不计),以同样的速度分别沿
处出发(小球的大小忽略不计),以同样的速度分别沿![]() 方向滚动,其终点分别是点
方向滚动,其终点分别是点![]() ,顺次连接四个小球所在的位置,得到四边形
,顺次连接四个小球所在的位置,得到四边形![]() .
.
(1)不论小球滚动多长时间,求证;四边形![]() 总是正方形;
总是正方形;
(2)这个四边形在什么时候面积最大?
(3)在什么时侯四边形![]() 的面积为正方形
的面积为正方形![]() 面积的一半?请说明理由.
面积的一半?请说明理由.
查看答案和解析>>
科目: 来源: 题型:
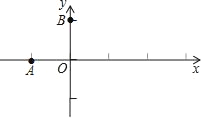
【题目】在平面直角坐标系xOy中,抛物线M:y=ax2+bx+c(a≠0)经过A(﹣1,0),且顶点坐标为B(0,1).
(1)求抛物线M的函数表达式;
(2)设F(t,0)为x轴正半轴上一点,将抛物线M绕点F旋转180°得到抛物线M1.
①抛物线M1的顶点B1的坐标为 ;
②当抛物线M1与线段AB有公共点时,结合函数的图象,求t的取值范围.
查看答案和解析>>
科目: 来源: 题型:
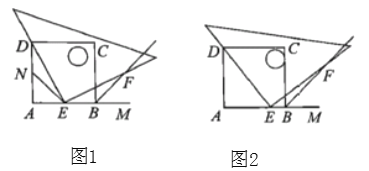
【题目】如图所示,四边形![]() 是正方形,
是正方形,![]() 是
是![]() 延长线上一点,直角三角尺的一条直角边经过点
延长线上一点,直角三角尺的一条直角边经过点![]() ,且直角顶点
,且直角顶点![]() 在
在![]() 边上滑动(点
边上滑动(点![]() 不与点
不与点![]() 重合),另一条直角边与
重合),另一条直角边与![]() 的平分线
的平分线![]() 相交于点
相交于点![]() .
.
(1)如图1所示,当点![]() 在
在![]() 边的中点时:
边的中点时:
①通过测量![]() 的长度,猜想
的长度,猜想![]() 与
与![]() 满足的数量关系是________________;
满足的数量关系是________________;
②连接点![]() 与
与![]() 边的中点
边的中点![]() ,猜想
,猜想![]() 与
与![]() 满足的数量关系是________________;
满足的数量关系是________________;
③请证明上述你的两个猜想.
(2)如图2所示,当点![]() 在
在![]() 边上的任意位置时,请你在
边上的任意位置时,请你在![]() 边上找到一点
边上找到一点![]() ,使得
,使得![]() ,进而猜想此时
,进而猜想此时![]() 与
与![]() 的数量关系.
的数量关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com