
科目: 来源: 题型:
【题目】已知AD为⊙O的直径,BC为⊙O的切线,切点为M,分别过A,D两点作BC的垂线,垂足分别为B,C,AD的延长线与BC相交于点E.
(1)求证:△ABM∽△MCD;
(2)若AD=8,AB=5,求ME的长.

查看答案和解析>>
科目: 来源: 题型:
【题目】班级组织同学乘大巴车前往“研学旅行”基地开展爱国教育活动,基地离学校有90公里,队伍8:00从学校出发.苏老师因有事情,8:30从学校自驾小车以大巴1.5倍的速度追赶,追上大巴后继续前行,结果比队伍提前15分钟到达基地.问:
(1)大巴与小车的平均速度各是多少?
(2)苏老师追上大巴的地点到基地的路程有多远?
查看答案和解析>>
科目: 来源: 题型:
【题目】湘西自治州风景优美,物产丰富,一外地游客到某特产专营店,准备购买精加工的豆腐乳和猕猴桃果汁两种盒装特产.若购买3盒豆腐乳和2盒猕猴桃果汁共需180元;购买1盒豆腐乳和3盒猕猴桃果汁共需165元.
(1)请分别求出每盒豆腐乳和每盒猕猴桃果汁的价格;
(2)该游客购买了4盒豆腐乳和2盒猕猴桃果汁,共需多少元?
查看答案和解析>>
科目: 来源: 题型:
【题目】密码锁有三个转轮,每个转轮上有十个数字:0,1,2,…9.小黄同学是9月份中旬出生,用生日“月份+日期”设置密码:9××
小张同学要破解其密码:
(1)第一个转轮设置的数字是9,第二个转轮设置的数字可能是 .
(2)请你帮小张同学列举出所有可能的密码,并求密码数能被3整除的概率;
(3)小张同学是6月份出生,根据(1)(2)的规律,请你推算用小张生日设置的密码的所有可能个数.
查看答案和解析>>
科目: 来源: 题型:
【题目】某校诗词知识竞赛培训活动中,在相同条件下对甲、乙两名学生进行了10次测验,他们的10次成绩如下(单位:分)

整理,分析过程如下:
成绩 学生 |
|
|
|
|
|
|
甲 | 0 | 1 | 4 | 5 | 0 | 0 |
乙 | 1 | 1 | 4 | 2 | 1 | 1 |
(1)两组数据的极差、平均数、中位数、众数、方差如下表所示,请补充完整:
学生 | 极差 | 平均数 | 中位数 | 众数 | 方差 |
甲 | 83.7 | 86 | 13.21 | ||
乙 | 24 | 83.7 | 82 | 46.21 |
(2)若从甲、乙两人中选择一人参加知识竞赛,你会选 (填“甲”或“乙”),理由为 .
查看答案和解析>>
科目: 来源: 题型:
【题目】如图是规格为![]() 的正方形网格,请在所给网格中按下列要求操作:
的正方形网格,请在所给网格中按下列要求操作:
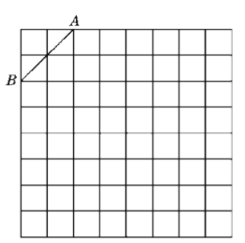
(1)请在网格中建立平面直角坐标系,使点A的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ;
;
(2)在第二象限内的格点上找一点![]() ,使点
,使点![]() 与线段
与线段![]() 组成一个以
组成一个以![]() 为底的等腰三角形,且腰长是无理数,画出
为底的等腰三角形,且腰长是无理数,画出![]() ,则点
,则点![]() 的坐标是 ,
的坐标是 ,![]() 的周长是 (结果保留根号);
的周长是 (结果保留根号);
(3)作出![]() 关于
关于![]() 轴对称的
轴对称的![]() .
.
查看答案和解析>>
科目: 来源: 题型:
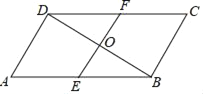
【题目】平行四边形ABCD中,∠A=60°,AB=2AD,BD的中垂线分别交AB,CD于点E,F,垂足为O.
(1)求证:OE=OF;
(2)若AD=6,求tan∠ABD的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,![]() 、
、![]() 、
、![]() 、…、
、…、![]() 均为等腰直角三角形,且
均为等腰直角三角形,且![]()
![]() ,点
,点![]() 、
、![]() 、
、![]() 、……、
、……、![]() 和点
和点![]() 、
、![]() 、
、![]() 、……、
、……、![]() 分别在正比例函数
分别在正比例函数![]() 和
和![]() 的图象上,且点
的图象上,且点![]() 、
、![]() 、
、![]() 、……、
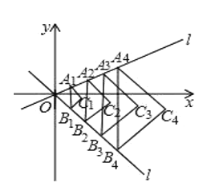
、……、![]() 的横坐标分别为1,2,3…
的横坐标分别为1,2,3…![]() ,线段
,线段![]() 、
、![]() 、
、![]() 、…、
、…、![]() 均与
均与![]() 轴平行.按照图中所反映的规律,则
轴平行.按照图中所反映的规律,则![]() 的顶点
的顶点![]() 的坐标是_____.(其中
的坐标是_____.(其中![]() 为正整数)
为正整数)
查看答案和解析>>
科目: 来源: 题型:
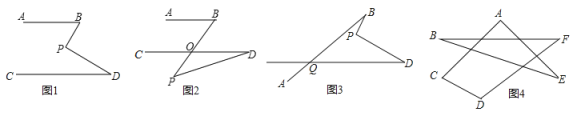
【题目】平面内的两条直线有相交和平行两种位置关系.
(1)如图1,若![]() ,点
,点![]() 在
在![]() 、
、![]() 内部,
内部,![]() ,
,![]() ,求
,求![]() 的度数.
的度数.
(2)如图2,在AB∥CD的前提下,将点![]() 移到
移到![]() 、
、![]() 外部,则
外部,则![]() 、
、![]() 、
、![]() 之间有何数量关系?请证明你的结论.
之间有何数量关系?请证明你的结论.
(3)如图3,写出![]() 、
、![]() 、
、![]() 、
、![]() 之间的数量关系?(不需证明)
之间的数量关系?(不需证明)
(4)如图4,求出![]() 的度数.
的度数.
查看答案和解析>>
科目: 来源: 题型:
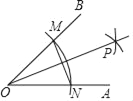
【题目】已知∠AOB=45°,求作∠AOP=22.5°,作法:
(1)以O为圆心,任意长为半径画弧分别交OA,OB于点N,M;
(2)分别以N,M为圆心,以OM长为半径在角的内部画弧交于点P;
(3)作射线OP,则OP为∠AOB的平分线,可得∠AOP=22.5°
根据以上作法,某同学有以下3种证明思路:
①可证明△OPN≌△OPM,得∠POA=∠POB,可得;
②可证明四边形OMPN为菱形,OP,MN互相垂直平分,得∠POA=∠POB,可得;
③可证明△PMN为等边三角形,OP,MN互相垂直平分,从而得∠POA=∠POB,可得.
你认为该同学以上3种证明思路中,正确的有( )
A. ①② B. ①③ C. ②③ D. ①②③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com