
科目: 来源: 题型:
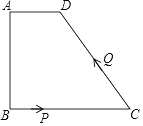
【题目】如图,四边形ABCD中,AD∥BC,∠A=90°,AD=1cm,AB=3cm,BC=5cm,动点P从点B出发以1cm/s的速度沿BC的方向运动,动点Q从点C出发以2cm/s的速度沿CD方向运动,P、Q两点同时出发,当Q到达点D时停止运动,点P也随之停止,设运动的时间为ts(t>0)
(1)求线段CD的长;
(2)t为何值时,线段PQ将四边形ABCD的面积分为1:2两部分?
查看答案和解析>>
科目: 来源: 题型:
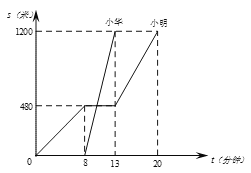
【题目】小明和小华是同班同学,也是邻居,某日早晨,小明7:40先出发去学校,走了一段后,在途中停下吃了早餐,后来发现上学时间快到了,就跑步到学校;小华离家后直接乘公共汽车到了学校.如图是他们从家到学校已走的路程s(米)和所用时间t(分钟)的关系图.则下列说法中
①小明家与学校的距离1200米;
②小华乘坐公共汽车的速度是240米/分;
③小华乘坐公共汽车后7:50与小明相遇;
④小华的出发时间不变,当小华由乘公共汽车变为跑步,且跑步的速度是100米/分时,他们可以同时到达学校.其中正确的个数是( )
A. 1 个B. 2个
C. 3 个D. 4个
查看答案和解析>>
科目: 来源: 题型:
【题目】黄岩某校搬迁后,需要增加教师和学生的寝室数量,寝室有三类,分别为单人间(供一个人住宿),双人间(供两个人住宿),四人间(供四个人住宿).因实际需要,单人间的数量在20至30之间(包括20和30),且四人间的数量是双人间的5倍.
(1)若2018年学校寝室数为64个,以后逐年增加,预计2020年寝室数达到121个,求2018至2020年寝室数量的年平均增长率;
(2)若三类不同的寝室的总数为121个,则最多可供多少师生住宿?
查看答案和解析>>
科目: 来源: 题型:
【题目】已知关于x的一元二次方程x2+(2m+1)x+m2﹣2=0.
(1)若该方程有两个实数根,求m的最小整数值;
(2)若方程的两个实数根为x1,x2,且(x1﹣x2)2+m2=21,求m的值.
查看答案和解析>>
科目: 来源: 题型:
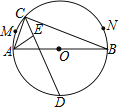
【题目】如图,![]() 是
是![]() 的直径,
的直径,![]() 、
、![]() 是弧
是弧![]() (异于
(异于![]() 、
、![]() )上两点,
)上两点,![]() 是弧
是弧![]() 上一动点,
上一动点,![]() 的角平分线交
的角平分线交![]() 于点
于点![]() ,
,![]() 的平分线交
的平分线交![]() 于点
于点![]() .当点
.当点![]() 从点
从点![]() 运动到点
运动到点![]() 时,则
时,则![]() 、
、![]() 两点的运动路径长的比是( )
两点的运动路径长的比是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,△ABC中,∠C=90°,AC=6,BC=8,动点P从A点出发,以1cm/s的速度,沿A—C—B向B点运动,同时,动点Q从C点出发,以2cm/s的速度,沿C—B—A向A点运动,当其中一点运动到终点时,两点同时停止运动。设运动时间为t秒,当t=_______秒时,△PCQ的面积等于8cm2.

查看答案和解析>>
科目: 来源: 题型:
【题目】我国边防局接到情报,近海处有一可疑船只A正向公海方向行驶,边防部迅速派出快艇B追赶(如图1).图2中l1、l2分别表示两船相対于海岸的距离s(海里)与追赶时间t(分)之间的关系.根据图象问答问题:
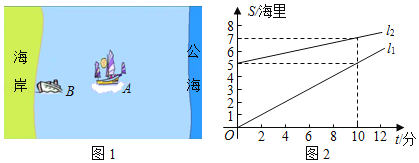
(1)①直线l1与直线l2中 表示B到海岸的距离与追赶时间之间的关系
②A与B比较, 速度快;
③如果一直追下去,那么B (填能或不能)追上A;
④可疑船只A速度是 海里/分,快艇B的速度是 海里/分
(2)l1与l2对应的两个一次函数表达式S1=k1t+b1与S2=k2t+b2中,k1、k2的实际意义各是什么?并直接写出两个具体表达式
(3)15分钟内B能否追上A?为什么?
(4)当A逃离海岸12海里的公海时,B将无法对其进行检查,照此速度,B能否在A逃入公海前将其拦截?为什么?
查看答案和解析>>
科目: 来源: 题型:
【题目】(2017甘肃省天水市)△ABC和△DEF是两个全等的等腰直角三角形,∠BAC=∠EDF=90°,△DEF的顶点E与△ABC的斜边BC的中点重合,将△DEF绕点E旋转,旋转过程中,线段DE与线段AB相交于点P,线段EF与射线CA相交于点Q.
(1)如图①,当点Q在线段AC上,且AP=AQ时,求证:△BPE≌△CQE;
(2)如图②,当点Q在线段CA的延长线上时,求证:△BPE∽△CEQ;并求当BP=2,CQ=9时BC的长.

查看答案和解析>>
科目: 来源: 题型:
【题目】已知:在梯形ABCD中,AD∥BC,∠ABC=90°,BC=2AD,E是BC的中点,连接AE、AC.
(1)点F是DC上一点,连接EF,交AC于点O(如图1),求证:△AOE∽△COF;
(2)若点F是DC的中点,连接BD,交AE与点G(如图2),求证:四边形EFDG是菱形.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com