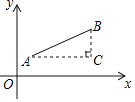
【题目】已知点A在x轴负半轴上，点B在y轴正半轴上，线段OB的长是方程x2﹣2x﹣8=0的解，tan∠BAO=．

（1）求点A的坐标；

（2）点E在y轴负半轴上，直线EC⊥AB，交线段AB于点C，交x轴于点D，S△DOE=16．若反比例函数y=的图象经过点C，求k的值；

（3）在（2）条件下，点M是DO中点，点N，P，Q在直线BD或y轴上，是否存在点P，使四边形MNPQ是矩形？若存在，请直接写出点P的坐标；若不存在，请说明理由．

请根据以上信息回答：

（1）本次参加抽样调查的居民有多少人？

（2）将两幅不完整的图补充完整；

（3）若居民区有8000人，请估计爱吃D粽的人数；

（4）若有外型完全相同的A、B、C、D粽各一个，煮熟后，小王吃了两个．用列表或画树状图的方法，求他第二个吃到的恰好是C粽的概率．

求y与x之间的关系．

若这些机械配件共获利1420元，请求出加工甲、乙、丙三种型号配件的人数分别是多少人？

A． B． C． D．

【题目】如图1，已知抛物线与x轴交于A、B两点，与y轴交于点C，顶点为D，连接BC

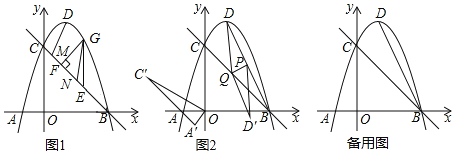
点G是直线BC上方抛物线上一动点不与B、C重合，过点G作y轴的平行线交直线BC于点E，作于点F，点M、N是线段BC上两个动点，且，连接DM、当的周长最大时，求的最小值；

如图2，连接BD，点P是线段BD的中点，点Q是线段BC上一动点，连接DQ，将沿PQ翻折，且线段的中点恰好落在线段BQ上，将绕点O逆时针旋转得到，点T为坐标平面内一点，当以点Q、、、T为顶点的四边形是平行四边形时，求点T的坐标．

【题目】某商店经销甲、乙两种商品现有如下信息：信息1：甲、乙两种商品的进货单价之和是3元；信息2：甲商品零售单价比进货单价多1元，乙商品零售单价比进货单价的2倍少1元；信息3：按零售单价购买甲商品3件和乙商品2件，共付了12元．请根据以上信息，解答下列问题：

求甲、乙两种商品的零售单价；

该商店平均每天卖出甲商品500件和乙商品1200件经调查发现，甲种商品零售单价每降元，甲种商品每天可多销售100件商店决定把甲种商品的零售单价下降元在不考虑其他因素的条件下，当m为多少时，商店每天销售甲、乙两种商品获取的总利润为1700元？

【题目】如图，在中，，点P从点B出发，沿折线运动，当它到达点A时停止，设点P运动的路程为点Q是射线CA上一点，，连接设，．

求出，与x的函数关系式，并注明x的取值范围；

补全表格中的值；

以表中各组对应值作为点的坐标，在直角坐标系内描出相应的点，并在x的取值范围内画出的函数图象：

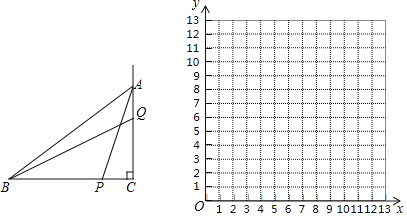
在直角坐标系内直接画出函数图象，结合和的函数图象，求出当时，x的取值范围．

收集数据：从三个年级中随机抽取了20个班级，学校对各班的评分如下：

92 71 89 82 69 82 96 83 77 83

80 82 66 73 82 78 92 70 74 59

整理、描述数据：按如下分数段整理、描述这两组样本数据：

说明：成绩90分及以上为优秀，分为良好，分为合格，60分以下为不合格

分析数据：样本数据的平均数、中位数、众数、极差如下表，绘制扇形统计图：

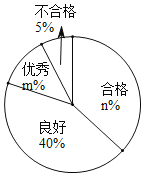
请根据以上信息解答下列问题：

填空：______，______，______，______．

若我校共120个班级，估计得分为优秀的班级有多少个？

为调动班级积极性，决定制定一个奖励标准分，凡到达或超过这个标准分的班级都将受到奖励如果要使得半数左右的班级都能获奖，奖励标准分应定为多少分？并简述其理由

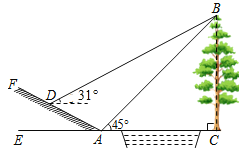
【题目】如图，小明为了测量小河对岸大树BC的高度，他在点A测得大树顶端B的仰角是45°，沿斜坡走米到达斜坡上点D，在此处测得树顶端点B的仰角为31°，且斜坡AF的坡比为1：2（参考数据：sin31°≈0.52，cos31°≈0.86，tan31°≈0.60）．

（1）求小明从点A走到点D的过程中，他上升的高度；

（2）大树BC的高度约为多少米？

材料一：我们将与称为一对“对偶式”因为，所以构造“对俩式”相乘可以有效地将和中的去掉.例如：已知，求 的值．解：，

材料二：如图，点，点，以AB为斜边作，则，于是，，所以.反之，可将代数式的值看作点到点的距离.

例如：=．

所以可将代数式的值看作点到点的距离．

利用材料一，解关于x的方程：，其中；

利用材料二，求代数式的最小值，并求出此时y与x的函数关系式，写出x的取值范图；

将所得的y与x的函数关系式和x的取值范围代入中解出x，直接写出x的值．