
科目: 来源: 题型:
【题目】如图1,抛物线![]() 交
交![]() 轴于点
轴于点![]() 和点
和点![]() ,交
,交![]() 轴于点
轴于点![]() ,一次函数
,一次函数![]() 的图象经过点
的图象经过点![]() ,
,![]() ,点
,点![]() 是抛物线上第二象限内一点.
是抛物线上第二象限内一点.
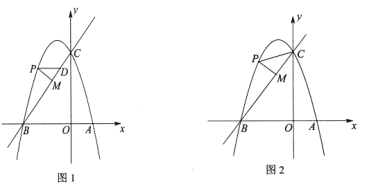
(1)求二次函数和一次函数的表达式;
(2)过点![]() 作
作![]() 轴的平行线交
轴的平行线交![]() 于点
于点![]() ,作
,作![]() 的垂线
的垂线![]() 交
交![]() 于点
于点![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() ,
,![]() 的周长为
的周长为![]() .
.
①求![]() 关于
关于![]() 的函数表达式;
的函数表达式;
②求![]() 的周长的最大值及此时点
的周长的最大值及此时点![]() 的坐标;
的坐标;
(3)如图2,连接![]() ,是否存在点
,是否存在点![]() ,使得以
,使得以![]() ,
,![]() ,
,![]() 为顶点的三角形与
为顶点的三角形与![]() 相似?若存在,直接写出点
相似?若存在,直接写出点![]() 的横坐标;若不存在,请说明理由.
的横坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】四边形的一条对角线把这个四边形分成了两个三角形,如果这两个三角形相似但不全等,我们就把这条对角线叫做这个四边形的“相似对角线”.
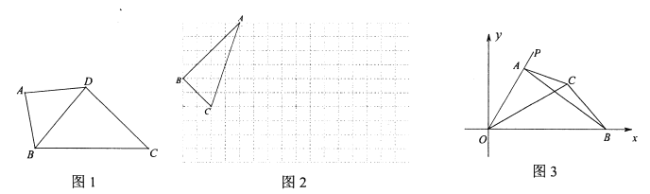
(1)如图1,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,对角线
,对角线![]() 平分
平分![]() .求证:
.求证:![]() 是四边形
是四边形![]() 的“相似对角线”;
的“相似对角线”;
(2)如图2,已知格点![]() ,请你在正方形网格中画出所有的格点四边形
,请你在正方形网格中画出所有的格点四边形![]() ,使四边形
,使四边形![]() 是以
是以![]() 为“相似对角线”的四边形;(注:顶点在小正方形顶点处的多边形称为格点多边形)
为“相似对角线”的四边形;(注:顶点在小正方形顶点处的多边形称为格点多边形)
(3)如图3,四边形![]() 中,点
中,点![]() 在射线
在射线![]() :
:![]() 上,点
上,点![]() 在
在![]() 轴正半轴上,对角线
轴正半轴上,对角线![]() 平分
平分![]() ,连接
,连接![]() .若
.若![]() 是四边形
是四边形![]() 的“相似对角线”,
的“相似对角线”,![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】某园林专业户计划投资种植花卉及树木,根据市场调查与预测,种植树木的利润![]() 与投资金额
与投资金额![]() 成正比例关系,如图1所示;种植花卉的利润
成正比例关系,如图1所示;种植花卉的利润![]() 与投资金额
与投资金额![]() 成二次函数关系,如图2所示.(注:利润与投资金额的单位均为万元)
成二次函数关系,如图2所示.(注:利润与投资金额的单位均为万元)
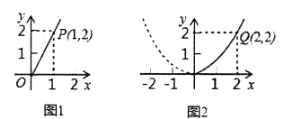
(1)分别求出利润![]() 与
与![]() 关于投资金额
关于投资金额![]() 的函数关系;
的函数关系;
(2)如果这位专业户以8万元资金投入种植花卉和树木,设他投入种植花卉的金额是![]() 万元,求这位专业户能获取的最大总利润是多少万元?
万元,求这位专业户能获取的最大总利润是多少万元?
查看答案和解析>>
科目: 来源: 题型:
【题目】某公园的人工湖边上有一座假山,假山顶上有一竖起的建筑物CD,高为10米,数学小组为了测量假山的高度DE,在公园找了一水平地面,在A处测得建筑物点D(即山顶)的仰角为35°,沿水平方向前进20米到达B点,测得建筑物顶部C点的仰角为45°,求假山的高度DE.(结果精确到1米,参考数据:sin35°≈![]() ,cos35°≈
,cos35°≈![]() ,tan35°≈
,tan35°≈![]() )
)
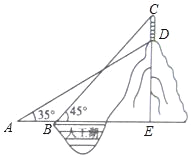
查看答案和解析>>
科目: 来源: 题型:
【题目】在三个完全相同的小球上分别写上-2,-1,2三个数字,然后装入一个不透明的布袋内搅匀,从布袋中取出一个球,记下小球上的数字为![]() ,放回袋中再搅匀,然后再从袋中取出一个小球,记下小球上的数字为
,放回袋中再搅匀,然后再从袋中取出一个小球,记下小球上的数字为![]() ,组成一对数
,组成一对数![]() .
.
(1)请用列表或画树状图的方法,表示出数对![]() 的所有可能的结果;
的所有可能的结果;
(2)求直线![]() 不经过第一象限的概率.
不经过第一象限的概率.
查看答案和解析>>
科目: 来源: 题型:
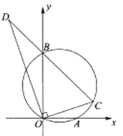
【题目】如图,在平面直角坐标系中,点![]() ,
,![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ,过
,过![]() ,
,![]() ,
,![]() 三点作圆,点
三点作圆,点![]() 在第一象限部分的圆上运动,连结
在第一象限部分的圆上运动,连结![]() ,过点
,过点![]() 作
作![]() 的垂线交
的垂线交![]() 的延长线于点
的延长线于点![]() ,下列说法:①
,下列说法:①![]() ;②
;②![]() ;③
;③![]() 的最大值为10.其中正确的是( )
的最大值为10.其中正确的是( )
A. ①②B. ②③C. ①③D. ①②③
查看答案和解析>>
科目: 来源: 题型:
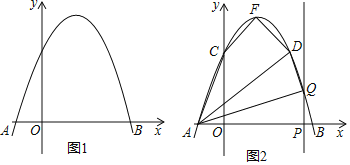
【题目】如图1,抛物线y=ax2+bx+3交x轴于点A(﹣1,0)和点B(3,0).
(1)求该抛物线所对应的函数解析式;
(2)如图2,该抛物线与y轴交于点C,顶点为F,点D(2,3)在该抛物线上.
①求四边形ACFD的面积;
②点P是线段AB上的动点(点P不与点A、B重合),过点P作PQ⊥x轴交该抛物线于点Q,连接AQ、DQ,当△AQD是直角三角形时,求出所有满足条件的点Q的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】问题提出
(1)如图①,在△ABC中,∠A=120°,AB=AC=5,则△ABC的外接圆半径R的值为 .
问题探究
(2)如图②,⊙O的半径为13,弦AB=24,M是AB的中点,P是⊙O上一动点,求PM的最大值.
问题解决
(3)如图③所示,AB、AC、BC是某新区的三条规划路其中,AB=6km,AC=3km,∠BAC=60°,BC所对的圆心角为60°.新区管委会想在BC路边建物资总站点P,在AB、AC路边分别建物资分站点E、F.也就是,分别在![]() 、线段AB和AC上选取点P、E、F.由于总站工作人员每天要将物资在各物资站点间按P→E→F→P的路径进行运输,因此,要在各物资站点之间规划道路PE、EF和FP.为了快捷环保和节约成本要使得线段PE、EF、FP之和最短,试求PE+EF+FP的最小值(各物资站点与所在道路之间的距离、路宽均忽略不计).
、线段AB和AC上选取点P、E、F.由于总站工作人员每天要将物资在各物资站点间按P→E→F→P的路径进行运输,因此,要在各物资站点之间规划道路PE、EF和FP.为了快捷环保和节约成本要使得线段PE、EF、FP之和最短,试求PE+EF+FP的最小值(各物资站点与所在道路之间的距离、路宽均忽略不计).

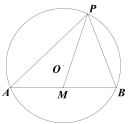

图① 图② 图③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com