
科目: 来源: 题型:
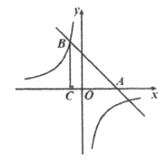
【题目】如图,在平面直角坐标系xOy中,直线![]() 与x轴交于点A,与双曲线
与x轴交于点A,与双曲线![]() 的一个交点为B(-1,4).
的一个交点为B(-1,4).
(1)求直线与双曲线的表达式;
(2)过点B作BC⊥x轴于点C,若点P在双曲线![]() 上,且△PAC的面积为4,求点P的坐标.
上,且△PAC的面积为4,求点P的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,四边形ABCD是矩形,点E在AD边上,点F在AD的延长线上,且BE=CF.
(1)求证:四边形EBCF是平行四边形.
(2)若∠BEC=90°,∠ABE=30°,AB=![]() ,求ED的长.
,求ED的长.

查看答案和解析>>
科目: 来源: 题型:
【题目】某林业部门统计某种树苗在本地区一定条件下的移植成活率,结果如表:
移植的棵数 | 300 | 700 | 1000 | 5000 | 15000 |
成活的棵数 | 280 | 622 | 912 | 4475 | 13545 |
成活的频率 | 0.933 | 0.889 | 0.912 | 0.895 | 0.903 |
根据表中的数据,估计这种树苗移植成活的概率为_____(精确到0.1);如果该地区计划成活4.5万棵幼树,那么需要移植这种幼树大约_____万棵.
查看答案和解析>>
科目: 来源: 题型:
【题目】下面是“已知底边及底边上的高线作等腰三角形”的尺规作图过程.
已知:线段![]() .求作:等腰
.求作:等腰![]() ,使
,使![]() ,
,![]() 边上的高为
边上的高为![]() .作法:如图,(1)作线段
.作法:如图,(1)作线段![]() ;(2)作线段
;(2)作线段![]() 的垂直平分线
的垂直平分线![]() 交
交![]() 于点
于点![]() ;(3)在射线
;(3)在射线![]() 上顺次截取线段
上顺次截取线段![]() ,连接
,连接![]() .所以
.所以![]() 即为所求作的等腰三角形.
即为所求作的等腰三角形.
请回答:得到![]() 是等腰三角形的依据是:
是等腰三角形的依据是:
①_____:
②_____.
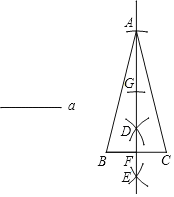
查看答案和解析>>
科目: 来源: 题型:
【题目】抛物线![]() (
(![]() 为常数)与
为常数)与![]() 轴交于点
轴交于点![]() 和
和![]() 与
与![]() 轴交于点
轴交于点![]() ,点
,点![]() 为抛物线顶点.
为抛物线顶点.
(Ⅰ)当![]() 时,求点
时,求点![]() ,点
,点![]() 的坐标;
的坐标;
(Ⅱ)①若顶点![]() 在直线
在直线![]() 上时,用含有
上时,用含有![]() 的代数式表示
的代数式表示![]() ;
;
②在①的前提下,当点![]() 的位置最高时,求抛物线的解析式;
的位置最高时,求抛物线的解析式;
(Ⅲ)若![]() ,当
,当![]() 满足
满足![]() 值最小时,求
值最小时,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
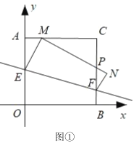
【题目】将一个正方形纸片![]() 放置在平面直角坐标系中,点
放置在平面直角坐标系中,点![]() ,点
,点![]() ,
,![]() ,
,![]() 点.动点
点.动点![]() 在边
在边![]() 上,点
上,点![]() 在边
在边![]() 上,沿
上,沿![]() 折叠该纸片,使点
折叠该纸片,使点![]() 的对应点
的对应点![]() 始终落在边
始终落在边![]() 上(点
上(点![]() 不与
不与![]() 重合),点
重合),点![]() 落在点
落在点![]() 处,
处,![]() 与
与![]() 交于点
交于点![]() .
.
(Ⅰ)如图①,当![]() 时,求点
时,求点![]() 的坐标;
的坐标;
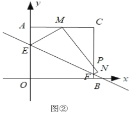
(Ⅱ)如图②,当点![]() 落在
落在![]() 的中点时,求点
的中点时,求点![]() 的坐标;
的坐标;
(Ⅲ)随着点![]() 在
在![]() 边上位置的变化,
边上位置的变化,![]() 的周长是否发生变化?如变化,简述理由;如不变,直接写出其值.
的周长是否发生变化?如变化,简述理由;如不变,直接写出其值.
查看答案和解析>>
科目: 来源: 题型:
【题目】甲、乙两个批发店销售同一种苹果,在甲批发店,不论一次购买数量是多少,价格均为6元/![]() .在乙批发店,一次购买数量不超过
.在乙批发店,一次购买数量不超过![]() 时,价格为7元/
时,价格为7元/![]() ;一次购买数量超过
;一次购买数量超过![]() 时,其中有
时,其中有![]() 的价格仍为7元/
的价格仍为7元/![]() ,超过
,超过![]() 部分的价格为5元/
部分的价格为5元/![]() .设小王在同一个批发店一次购买苹果的数量为
.设小王在同一个批发店一次购买苹果的数量为![]() .
.
(Ⅰ)根据题意填空:
①若一次购买数量为![]() 时,在甲批发店的花费为________元,在乙批发店的花费为________元;
时,在甲批发店的花费为________元,在乙批发店的花费为________元;
②若一次购买数量为![]() 时,在甲批发店的花费为________元,在乙批发店的花费为________元;
时,在甲批发店的花费为________元,在乙批发店的花费为________元;
(Ⅱ)设在甲批发店花费![]() 元,在乙批发店花费
元,在乙批发店花费![]() 元,分别求
元,分别求![]() ,
,![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(Ⅲ)根据题意填空:
①若小王在甲批发店和在乙批发店一次购买苹果的数量相同,且花费相同,则他在同一个批发店一次购买苹果的数量为_________![]() ;
;
②若小王在同一个批发店一次购买苹果的数量为![]() ,则他在甲、乙两个批发店中的________批发店购买花费少;
,则他在甲、乙两个批发店中的________批发店购买花费少;
③若小王在同一个批发店一次购买苹果花费了260元,则他在甲、乙两个批发店中的_________批发店购买数量多.
查看答案和解析>>
科目: 来源: 题型:
【题目】为了推动阳光体育运动的广泛开展,引导学生走向操场、走进大自然、走到阳光下,积极参加体育锻炼,学校准备购买一批运动鞋供学生借用.现从各年级随机抽取了部分学生的鞋号,绘制出如下的统计图①和图②,请根据相关信息,解答下列问题:
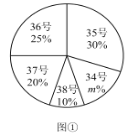
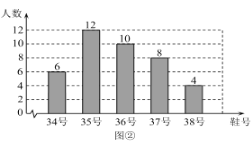
(Ⅰ)本次接受随机抽样调查的学生人数为________,图①中![]() 的值为________;
的值为________;
(Ⅱ)求本次调查获取的样本数据的众数和中位数;
(Ⅲ)根据样本数据,若学校计划购买150双运动鞋,建议购买35号运动鞋多少双?
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线![]() 与直线
与直线![]() 有两个不同的交点.下列结论:①
有两个不同的交点.下列结论:①![]() ;②当
;②当![]() 时,
时,![]() 有最小值
有最小值![]() ;③方程
;③方程![]() 有两个不等实根;④若连接这两个交点与抛物线的顶点,恰好是一个等腰直角三角形,则
有两个不等实根;④若连接这两个交点与抛物线的顶点,恰好是一个等腰直角三角形,则![]() ;其中正确的结论的个数是( )
;其中正确的结论的个数是( )
A.4B.3C.2D.1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com