
【题目】将一个正方形纸片![]() 放置在平面直角坐标系中,点
放置在平面直角坐标系中,点![]() ,点
,点![]() ,
,![]() ,
,![]() 点.动点
点.动点![]() 在边
在边![]() 上,点
上,点![]() 在边
在边![]() 上,沿
上,沿![]() 折叠该纸片,使点
折叠该纸片,使点![]() 的对应点
的对应点![]() 始终落在边
始终落在边![]() 上(点
上(点![]() 不与
不与![]() 重合),点
重合),点![]() 落在点
落在点![]() 处,
处,![]() 与
与![]() 交于点
交于点![]() .
.
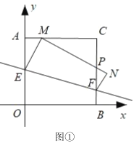
(Ⅰ)如图①,当![]() 时,求点
时,求点![]() 的坐标;
的坐标;
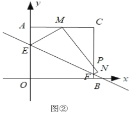
(Ⅱ)如图②,当点![]() 落在
落在![]() 的中点时,求点
的中点时,求点![]() 的坐标;
的坐标;
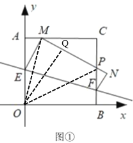
(Ⅲ)随着点![]() 在
在![]() 边上位置的变化,
边上位置的变化,![]() 的周长是否发生变化?如变化,简述理由;如不变,直接写出其值.
的周长是否发生变化?如变化,简述理由;如不变,直接写出其值.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() ;(Ⅲ)不变,
;(Ⅲ)不变,![]() 的周长为8.
的周长为8.
【解析】
(Ⅰ)根据含30°直角三角形的性质以及勾股定理,在Rt△AEM中运用勾股定理列出方程即可解答;
(Ⅱ)由题意可得AM=MC=2,设AE=a,则OE=EM=4-a,在Rt△AEM中,利用勾股定理列出方程即可解答;
(Ⅲ)如图,连接OM,OP,过点O作OQ⊥MP于点Q,由折叠的性质及平行线的性质得到∠MOB=∠OMP,进而证明△AMO≌△QMO(AAS),得到AM=QM,AO=QO,再证明Rt△QOP≌Rt△BOP(HL),得到QP=BP,将△MPC的周长进行转化即可得到AC+BC=8即可.
解:(Ⅰ)当![]() 时,
时,
∵四边形AOBC是正方形,
∴∠OAC=90°,
∴AM=![]() ,
,
由折叠可知,OE=EM,
设AM=x,则EM=OE=2x,
∵![]() ,
,
∴OA=4,
∴AE=4-2x,
在Rt△AEM中,AM2+AE2=EM2,
即![]() ,解得:
,解得:![]() ,
,![]() (舍去)
(舍去)
∴OE=2x=![]() ,
,
∴![]() ;
;
(Ⅱ)∵AC=4,
∴当点![]() 落在
落在![]() 的中点时,AM=MC=2,
的中点时,AM=MC=2,
设AE=a,则OE=EM=4-a,
则在Rt△AEM中,AM2+AE2=EM2,
即![]() ,解得:
,解得:![]() ,
,
∴OE=![]() ,
,
∴![]() ;
;
(Ⅲ)不变,![]() 的周长为8,
的周长为8,
如图,连接OM,OP,过点O作OQ⊥MP于点Q,
由折叠可知,∠EMP=∠AOB=90°,OE=EM,
∴∠EOM=∠EMO,
∴90°-∠EOM=90°-∠EMO,即∠MOB=∠OMP,
又∵正方形AOBC中,AC∥OB,
∴∠AMO=∠MOB,
∴∠AMO=∠OMP,
在△AMO与△QMO中,
∠OAM=∠OQM=90°,∠AMO=∠OMQ,OM=OM,
∴△AMO≌△QMO(AAS),
∴AM=QM,AO=QO,
又∵AO=BO,
∴QO=BO,
∴在Rt△QOP与Rt△BOP中,
OP=OP,QO=BO,
∴Rt△QOP≌Rt△BOP(HL),
∴QP=BP,
∴![]() 的周长=MC+PC+MP
的周长=MC+PC+MP
=MC+PC+MQ+QP
=MC+AM+PC+BP
=AC+BC
=8
∴随着点![]() 在
在![]() 边上位置的变化,
边上位置的变化,![]() 的周长不变,周长为8.
的周长不变,周长为8.


 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案科目:初中数学 来源: 题型:
【题目】据交管部门统计,高速公路超速行驶是引发交通事故的主要原因.我县某校数学课外小组的几个同学想尝试用自己所学的知识检测车速,渝黔高速公路某路段的限速是:每小时80千米(即最高时速不超过80千米),如图,他们将观测点设在到公路l的距离为0.1千米的P处.这时,一辆轿车由綦江向重庆匀速直线驶来,测得此车从A处行驶到B处所用的时间为3秒(注:3秒=![]() 小时),并测得∠APO=59°,∠BPO=45°.试计算AB并判断此车是否超速?(精确到0.001).(参考数据:sin59°≈0.8572,cos59°≈0.5150,tan59°≈1.6643)
小时),并测得∠APO=59°,∠BPO=45°.试计算AB并判断此车是否超速?(精确到0.001).(参考数据:sin59°≈0.8572,cos59°≈0.5150,tan59°≈1.6643)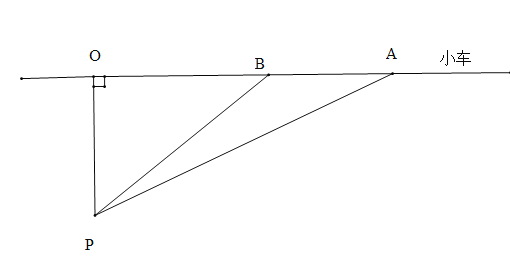
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某次数学测验中,一道题满分3分,老师评分只给整数,即得分只能为0分,1分,2分,3分.李老师为了了解学生得分情况和试题的难易情况,对初三(1)班所有学生的试题进行了分析整理,并绘制了两幅尚不完整的统计图,如图所示.

解答下列问题:
(1)m= ,n= ,并补全条形统计图;
(2)在初三(1)班随机抽取一名学生的成绩,求抽中的成绩为得分众数的概率;
(3)根据右侧“小知识”,通过计算判断这道题对于该班级来说,属于哪一类难度的试题?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 上有一点
上有一点![]() ,
,![]() 的横坐标为1,过
的横坐标为1,过![]() 作
作![]() 轴,与抛物线的另一个交点为
轴,与抛物线的另一个交点为![]() ,且
,且![]() ,作
,作![]() 轴,垂足为
轴,垂足为![]() ,抛物线与
,抛物线与![]() 轴正半轴交于点
轴正半轴交于点![]() ,连结
,连结![]() ,
,![]() 与
与![]() 交于点
交于点![]() .
.
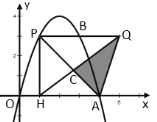
(1)当![]() 时,①求点
时,①求点![]() 的坐标:②求
的坐标:②求![]() 的面积:
的面积:
(2)当![]() 是以
是以![]() 为腰的等腰三角形时,求
为腰的等腰三角形时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点到直线的距离即为点到直线的垂线段的长.

(1)如图1,取点M(1,0),则点M到直线l:y=![]() x﹣1的距离为多少?
x﹣1的距离为多少?
(2)如图2,点P是反比例函数y=![]() 在第一象限上的一个点,过点P分别作PM⊥x轴,作PN⊥y轴,记P到直线MN的距离为d0,问是否存在点P,使d0=
在第一象限上的一个点,过点P分别作PM⊥x轴,作PN⊥y轴,记P到直线MN的距离为d0,问是否存在点P,使d0=![]() ?若存在,求出点P的坐标,若不存在,请说明理由.
?若存在,求出点P的坐标,若不存在,请说明理由.
(3)如图3,若直线y=kx+m与抛物线y=x2﹣4x相交于x轴上方两点A、B(A在B的左边).且∠AOB=90°,求点P(2,0)到直线y=kx+m的距离最大时,直线y=kx+m的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
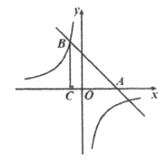
【题目】如图,在平面直角坐标系xOy中,直线![]() 与x轴交于点A,与双曲线
与x轴交于点A,与双曲线![]() 的一个交点为B(-1,4).
的一个交点为B(-1,4).
(1)求直线与双曲线的表达式;
(2)过点B作BC⊥x轴于点C,若点P在双曲线![]() 上,且△PAC的面积为4,求点P的坐标.
上,且△PAC的面积为4,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,D、E分别在边AB、AC上,下列条件中,不能确定△ADE∽△ACB的是( )
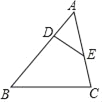
A. ∠AED=∠B B. ∠BDE+∠C=180°
C. ADBC=ACDE D. ADAB=AEAC
查看答案和解析>>
科目:初中数学 来源: 题型:
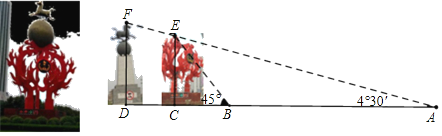
【题目】“马踏飞燕”作为商丘的地标性雕塑被拆分为两座雕塑,安放在紧邻高速公路出站口的平原路和华商大道交叉口,不光临近古城景区,也靠近火神台,恰恰实现了商丘市的城市文化宣传的目的.“人们来到商丘,一下高速,就看到商丘的地标,就能够感受到商丘的火文化.”
某中学数学兴趣小组准备测量安放后的雕塑相关数据,如图,小明从A点测得“火球”最高点E的仰角为4°30′,此处恰好看不到“马踏飞燕”雕塑的最高点F,小明向雕塑走140m到达点B,此时测得点E的仰角为45°.已知两雕塑的距离为50m,求两座雕塑EC、FD的高度.(A、B、C、D在同一直线上)(精确到1m,参考值:sin4°30′≈0.07,cos4°30′≈0.99,tan4°30′≈0.08.)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com