
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕжаЃЌЕуЕНжБЯпЕФОрРыМДЮЊЕуЕНжБЯпЕФДЙЯпЖЮЕФГЄЃЎ

ЃЈ1ЃЉШчЭМ1ЃЌШЁЕуMЃЈ1ЃЌ0ЃЉЃЌдђЕуMЕНжБЯпlЃКyЃН![]() xЉ1ЕФОрРыЮЊЖрЩйЃП
xЉ1ЕФОрРыЮЊЖрЩйЃП
ЃЈ2ЃЉШчЭМ2ЃЌЕуPЪЧЗДБШР§КЏЪ§yЃН![]() дкЕквЛЯѓЯоЩЯЕФвЛИіЕуЃЌЙ§ЕуPЗжБ№зїPMЁЭxжсЃЌзїPNЁЭyжсЃЌМЧPЕНжБЯпMNЕФОрРыЮЊd0ЃЌЮЪЪЧЗёДцдкЕуPЃЌЪЙd0ЃН
дкЕквЛЯѓЯоЩЯЕФвЛИіЕуЃЌЙ§ЕуPЗжБ№зїPMЁЭxжсЃЌзїPNЁЭyжсЃЌМЧPЕНжБЯпMNЕФОрРыЮЊd0ЃЌЮЪЪЧЗёДцдкЕуPЃЌЪЙd0ЃН![]() ЃПШєДцдкЃЌЧѓГіЕуPЕФзјБъЃЌШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЃПШєДцдкЃЌЧѓГіЕуPЕФзјБъЃЌШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЃЈ3ЃЉШчЭМ3ЃЌШєжБЯпyЃНkx+mгыХзЮяЯпyЃНx2Љ4xЯрНЛгкxжсЩЯЗНСНЕуAЁЂBЃЈAдкBЕФзѓБпЃЉЃЎЧвЁЯAOBЃН90ЁуЃЌЧѓЕуPЃЈ2ЃЌ0ЃЉЕНжБЯпyЃНkx+mЕФОрРызюДѓЪБЃЌжБЯпyЃНkx+mЕФНтЮіЪНЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉЕуPЃЈ
ЃЛЃЈ2ЃЉЕуPЃЈ![]() ЃЌ2
ЃЌ2![]() ЃЉЛђЃЈ2
ЃЉЛђЃЈ2![]() ЃЌ
ЃЌ![]() ЃЉЃЛЃЈ3ЃЉyЃНЉ2x+9
ЃЉЃЛЃЈ3ЃЉyЃНЉ2x+9
ЁОНтЮіЁП
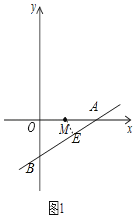
ЃЈ1ЃЉШчЭМ1ЃЌЩшжБЯпlЃКyЃН![]() xЉ1гыxжсЃЌyжсЕФНЛЕуЮЊЕуAЃЌЕуBЃЌЙ§ЕуMзїMEЁЭABЃЌЯШЧѓГіЕуAЃЌЕуBзјБъЃЌПЩЕУOAЃН2ЃЌOBЃН1ЃЌAMЃН1ЃЌгЩЙДЙЩЖЈРэПЩЧѓABГЄЃЌгЩШёНЧШ§НЧКЏЪ§ПЩЧѓНтЃЛ
xЉ1гыxжсЃЌyжсЕФНЛЕуЮЊЕуAЃЌЕуBЃЌЙ§ЕуMзїMEЁЭABЃЌЯШЧѓГіЕуAЃЌЕуBзјБъЃЌПЩЕУOAЃН2ЃЌOBЃН1ЃЌAMЃН1ЃЌгЩЙДЙЩЖЈРэПЩЧѓABГЄЃЌгЩШёНЧШ§НЧКЏЪ§ПЩЧѓНтЃЛ
ЃЈ2ЃЉЩшЕуPЃЈaЃЌ![]() ЃЉЃЌгУВЮЪ§aБэЪОMNЕФГЄЃЌгЩУцЛ§ЙиЯЕПЩЧѓaЕФжЕЃЌМДПЩЧѓЕуPзјБъЃЛ
ЃЉЃЌгУВЮЪ§aБэЪОMNЕФГЄЃЌгЩУцЛ§ЙиЯЕПЩЧѓaЕФжЕЃЌМДПЩЧѓЕуPзјБъЃЛ
ЃЈ3ЃЉШчЭМ3ЃЌЙ§ЕуAзїACЁЭxжсгкЕуCЃЌЙ§ЕуBзїBDЁЭyжсгкЕуDЃЌЩшЕуAЃЈaЃЌa2Љ4aЃЉЃЌЕуBЃЈbЃЌb2Љ4bЃЉЃЌЭЈЙ§жЄУїЁїAOCЁзЁїBODЃЌПЩЕУabЉ4ЃЈa+bЃЉ+17ЃН0ЃЌгЩИљгыЯЕЪ§ЙиЯЕПЩЧѓa+bЃНk+4ЃЌabЃНЉmЃЌПЩЕУyЃНkx+1Љ4kЃНkЃЈxЉ4ЃЉ+1ЃЌПЩЕУжБЯпyЃНkЃЈxЉ4ЃЉ+1Й§ЖЈЕуNЃЈ4ЃЌ1ЃЉЃЌдђЕБPNЁЭжБЯпyЃНkx+mЪБЃЌЕуPЕНжБЯпyЃНkx+mЕФОрРызюДѓЃЌгЩД§ЖЈЯЕЪ§ЗЈПЩЧѓжБЯпPNЕФНтЮіЪНЃЌПЩЧѓkЃЌmЕФжЕЃЌМДПЩЧѓНтЃЎ
НтЃКЃЈ1ЃЉШчЭМ1ЃЌЩшжБЯпlЃКyЃН![]() xЉ1гыxжсЃЌyжсЕФНЛЕуЮЊЕуAЃЌЕуBЃЌЙ§ЕуMзїMEЁЭABЃЌ
xЉ1гыxжсЃЌyжсЕФНЛЕуЮЊЕуAЃЌЕуBЃЌЙ§ЕуMзїMEЁЭABЃЌ
ЁпжБЯпlЃКyЃН![]() xЉ1гыxжсЃЌyжсЕФНЛЕуЮЊЕуAЃЌЕуBЃЌ
xЉ1гыxжсЃЌyжсЕФНЛЕуЮЊЕуAЃЌЕуBЃЌ
ЁрЕуAЃЈ2ЃЌ0ЃЉЃЌЕуBЃЈ0ЃЌЉ1ЃЉЃЌЧвЕуMЃЈ1ЃЌ0ЃЉЃЌ
ЁрAOЃН2ЃЌBOЃН1ЃЌAMЃНOMЃН1ЃЌ
ЁрABЃН![]() ЃН
ЃН![]() ЃН
ЃН![]() ЃЌ
ЃЌ
ЁпtanЁЯOABЃНtanЁЯMAEЃН![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁрMEЃН![]() ЃЌ
ЃЌ
ЁрЕуMЕНжБЯпlЃКyЃН![]() xЉ1ЕФОрРыЮЊ
xЉ1ЕФОрРыЮЊ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЩшЕуPЃЈaЃЌ![]() ЃЉЃЌЃЈaЃО0ЃЉ
ЃЉЃЌЃЈaЃО0ЃЉ
ЁрOMЃНaЃЌONЃН![]() ЃЌ
ЃЌ
ЁрMNЃН![]() ЃН
ЃН![]() ЃЌ
ЃЌ
ЁпPMЁЭxжсЃЌPNЁЭyжсЃЌЁЯMONЃН90ЁуЃЌ
ЁрЫФБпаЮPMONЪЧОиаЮЃЌ
ЁрSЁїPMNЃН![]() SОиаЮPMONЃН2ЃЌ
SОиаЮPMONЃН2ЃЌ
Ёр![]() ЁСMNЁСd0ЃН2ЃЌ
ЁСMNЁСd0ЃН2ЃЌ
Ёр![]() ЁС
ЁС![]() ЃН4ЃЌ
ЃН4ЃЌ
Ёрa4Љ10a2+16ЃН0ЃЌ
Ёрa1ЃН2ЃЌa2ЃНЉ2ЃЈЩсШЅЃЉЃЌa3ЃН2![]() ЃЌa4ЃНЉ2
ЃЌa4ЃНЉ2![]() ЃЈЩсШЅЃЉЃЌ
ЃЈЩсШЅЃЉЃЌ
ЁрЕуPЃЈ![]() ЃЌ2
ЃЌ2![]() ЃЉЛђЃЈ2
ЃЉЛђЃЈ2![]() ЃЌ
ЃЌ![]() ЃЉЃЌ
ЃЉЃЌ
ЃЈ3ЃЉШчЭМ3ЃЌЙ§ЕуAзїACЁЭxжсгкЕуCЃЌЙ§ЕуBзїBDЁЭyжсгкЕуDЃЌ
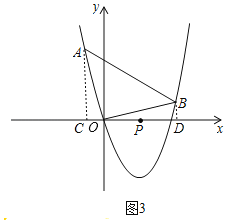
ЩшЕуAЃЈaЃЌa2Љ4aЃЉЃЌЕуBЃЈbЃЌb2Љ4bЃЉЃЌ
ЁпЁЯAOBЃН90ЁуЃЌ
ЁрЁЯAOC+ЁЯBODЃН90ЁуЃЌЧвЁЯAOC+ЁЯCAOЃН90ЁуЃЌ
ЁрЁЯBODЃНЁЯCAOЃЌЧвЁЯACOЃНЁЯBDOЃЌ
ЁрЁїAOCЁзЁїBODЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]()
ЁрabЉ4ЃЈa+bЃЉ+17ЃН0ЃЌ
ЁпжБЯпyЃНkx+mгыХзЮяЯпyЃНx2Љ4xЯрНЛгкxжсЩЯЗНСНЕуAЁЂBЃЌ
ЁрaЃЌbЪЧЗНГЬkx+mЃНx2Љ4xЕФСНИљЃЌ
Ёрa+bЃНk+4ЃЌabЃНЉmЃЌ
ЁрЉmЉ4ЃЈk+4ЃЉ+17ЃН0ЃЌ
ЁрmЃН1Љ4kЃЌ
ЁрyЃНkx+1Љ4kЃНkЃЈxЉ4ЃЉ+1ЃЌ
ЁржБЯпyЃНkЃЈxЉ4ЃЉ+1Й§ЖЈЕуNЃЈ4ЃЌ1ЃЉЃЌ
ЁрЕБPNЁЭжБЯпyЃНkx+mЪБЃЌЕуPЕНжБЯпyЃНkx+mЕФОрРызюДѓЃЌ
ЩшжБЯпPNЕФНтЮіЪНЮЊyЃНcx+dЃЌ
Ёр![]()
НтЕУ
ЁржБЯпPNЕФНтЮіЪНЮЊyЃН![]() xЉ1ЃЌ
xЉ1ЃЌ
ЁрkЃНЉ2ЃЌ
ЁрmЃН1Љ4ЁСЃЈЉ2ЃЉЃН9ЃЌ
ЁржБЯпyЃНkx+mЕФНтЮіЪНЮЊyЃНЉ2x+9ЃЎ


 ЯАЬтОЋбЁЯЕСаД№АИ
ЯАЬтОЋбЁЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌ![]() ЃЌ
ЃЌ![]() ЮЊ
ЮЊ![]() жаЕуЃЌЕу
жаЕуЃЌЕу![]() ЮЊЩфЯп
ЮЊЩфЯп![]() ЩЯЃЈВЛгыЕу
ЩЯЃЈВЛгыЕу![]() жиКЯЃЉЕФШЮвтвЛЕуЃЌСЌНг
жиКЯЃЉЕФШЮвтвЛЕуЃЌСЌНг![]() ЃЌВЂЪЙ
ЃЌВЂЪЙ![]() ЕФбгГЄЯпНЛЩфЯп
ЕФбгГЄЯпНЛЩфЯп![]() гкЕу
гкЕу![]() ЃЌЩш
ЃЌЩш![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓжЄЃК![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЕБ![]() ЪБЃЌЧѓ
ЪБЃЌЧѓ![]() ЕФГЄЃЛ
ЕФГЄЃЛ
ЃЈ3ЃЉЕБ![]() ЕФЭтаФВЛдкШ§НЧаЮЭтВПЪБЃЌЧыжБНгаДГі
ЕФЭтаФВЛдкШ§НЧаЮЭтВПЪБЃЌЧыжБНгаДГі![]() ЕФШЁжЕЗЖЮЇЃЎ
ЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
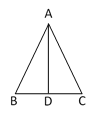
ЁОЬтФПЁПдкжЄУїЕШбќШ§НЧаЮЕФХаЖЈЖЈРэЁАЕШНЧЖдЕШБпЁБЃЌМДЁАШчЭМЃЌвбжЊЃКЁЯB=ЁЯCЃЌЧѓжЄЃКAB=ACЁБЪБЃЌаЁУїзїСЫШчЯТЕФИЈжњЯпЃЌЯТСаЖдИЈжњЯпЕФУшЪіе§ШЗЕФгаЃЈ ЃЉ
ЂйзїЁЯBACЕФЦНЗжЯпADНЛBCгкЕуDЂкШЁBCБпЕФжаЕуDЃЌСЌНгADЂлЙ§ЕуAзїADЁЭBCЃЌДЙзуЮЊЕуDЂмзїBCБпЕФДЙжБЦНЗжЯпADЃЌНЛBCгкЕуD
A.1ИіB.2ИіC.3ИіD.4Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
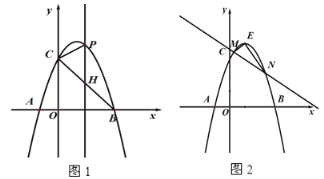
ЁОЬтФПЁПШчЭМ1ЃЌвбжЊХзЮяЯп![]() гы
гы![]() жсНЛгкЕу
жсНЛгкЕу![]() ЃЌгы
ЃЌгы![]() жсНЛгкЕу
жсНЛгкЕу![]() ЃЎ
ЃЎ
 ЁЁЁЁЁЁ
ЁЁЁЁЁЁ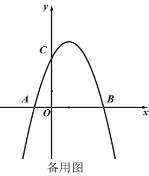
ЃЈ1ЃЉЧѓ![]() ЃЌ
ЃЌ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ2ЃЉЕу![]() ЪЧЕквЛЯѓЯоХзЮяЯпЩЯвЛЖЏЕуЃЌЙ§Еу
ЪЧЕквЛЯѓЯоХзЮяЯпЩЯвЛЖЏЕуЃЌЙ§Еу![]() зї
зї![]() жсЕФДЙЯп
жсЕФДЙЯп![]() ЃЌНЛ
ЃЌНЛ![]() гкЕу
гкЕу![]() ЃЎЕБЁї
ЃЎЕБЁї![]() ЮЊЕШбќШ§НЧаЮЪБЃЌЧѓЕу
ЮЊЕШбќШ§НЧаЮЪБЃЌЧѓЕу![]() ЕФзјБъЃЛ
ЕФзјБъЃЛ
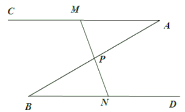
ЃЈ3ЃЉШчЭМ2ЃЌХзЮяЯпЖЅЕуЮЊ![]() ЃЌвбжЊжБЯп
ЃЌвбжЊжБЯп![]() гыЖўДЮКЏЪ§ЭМЯѓЯрНЛгк
гыЖўДЮКЏЪ§ЭМЯѓЯрНЛгк![]() ЃЌ
ЃЌ![]() СНЕуЃЎЧѓжЄЃКЮоТл
СНЕуЃЎЧѓжЄЃКЮоТл![]() ЮЊКЮжЕЃЌЁї
ЮЊКЮжЕЃЌЁї![]() КуЮЊжБНЧШ§НЧаЮЃЎ
КуЮЊжБНЧШ§НЧаЮЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЎдк![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЪЧ
ЪЧ![]() ЕФжаЮЛЯпЃЌСЌНс
ЕФжаЮЛЯпЃЌСЌНс![]() ЃЌЕу
ЃЌЕу![]() ЪЧБп
ЪЧБп![]() ЩЯЕФвЛИіЖЏЕуЃЌСЌНс
ЩЯЕФвЛИіЖЏЕуЃЌСЌНс![]() НЛ
НЛ![]() гк
гк![]() ЃЌНЛ
ЃЌНЛ![]() гк
гк![]() ЃЎ
ЃЎ
(1)ЕБЕу![]() ЪЧ
ЪЧ![]() ЕФжаЕуЪБЃЌЧѓ
ЕФжаЕуЪБЃЌЧѓ![]() ЕФжЕМА
ЕФжЕМА![]() ЕФГЄ
ЕФГЄ
(2) ЕБЫФБпаЮ![]() гыЫФБпаЮ
гыЫФБпаЮ![]() ЕФУцЛ§ЯрЕШЪБЃЌЧѓ
ЕФУцЛ§ЯрЕШЪБЃЌЧѓ![]() ЕФГЄЃК
ЕФГЄЃК
(3)ШчЭМ2ЃЎвд![]() ЮЊжБОЖзї
ЮЊжБОЖзї![]() ЃЎ
ЃЎ
ЂйЕБ![]() е§КУОЙ§Еу
е§КУОЙ§Еу![]() ЪБЃЌЧѓжЄЃК
ЪБЃЌЧѓжЄЃК![]() ЪЧ
ЪЧ![]() ЕФЧаЯпЃК
ЕФЧаЯпЃК
ЂкЕБ![]() ЕФжЕТњзуЪВУДЬѕМўЪБЃЌ
ЕФжЕТњзуЪВУДЬѕМўЪБЃЌ![]() гыЯпЖЮ
гыЯпЖЮ![]() гаЧвжЛгавЛИіНЛЕуЃЎ
гаЧвжЛгавЛИіНЛЕуЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
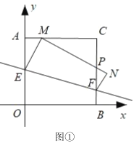
ЁОЬтФПЁПНЋвЛИіе§ЗНаЮжНЦЌ![]() ЗХжУдкЦНУцжБНЧзјБъЯЕжаЃЌЕу
ЗХжУдкЦНУцжБНЧзјБъЯЕжаЃЌЕу![]() ЃЌЕу
ЃЌЕу![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЕуЃЎЖЏЕу
ЕуЃЎЖЏЕу![]() дкБп
дкБп![]() ЩЯЃЌЕу
ЩЯЃЌЕу![]() дкБп
дкБп![]() ЩЯЃЌби
ЩЯЃЌби![]() елЕўИУжНЦЌЃЌЪЙЕу
елЕўИУжНЦЌЃЌЪЙЕу![]() ЕФЖдгІЕу
ЕФЖдгІЕу![]() ЪМжеТфдкБп
ЪМжеТфдкБп![]() ЩЯЃЈЕу
ЩЯЃЈЕу![]() ВЛгы
ВЛгы![]() жиКЯЃЉЃЌЕу
жиКЯЃЉЃЌЕу![]() ТфдкЕу
ТфдкЕу![]() ДІЃЌ
ДІЃЌ![]() гы
гы![]() НЛгкЕу
НЛгкЕу![]() ЃЎ
ЃЎ
ЃЈЂёЃЉШчЭМЂйЃЌЕБ![]() ЪБЃЌЧѓЕу
ЪБЃЌЧѓЕу![]() ЕФзјБъЃЛ
ЕФзјБъЃЛ
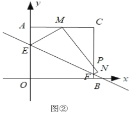
ЃЈЂђЃЉШчЭМЂкЃЌЕБЕу![]() Тфдк
Тфдк![]() ЕФжаЕуЪБЃЌЧѓЕу
ЕФжаЕуЪБЃЌЧѓЕу![]() ЕФзјБъЃЛ
ЕФзјБъЃЛ
ЃЈЂѓЃЉЫцзХЕу![]() дк
дк![]() БпЩЯЮЛжУЕФБфЛЏЃЌ
БпЩЯЮЛжУЕФБфЛЏЃЌ![]() ЕФжмГЄЪЧЗёЗЂЩњБфЛЏЃПШчБфЛЏЃЌМђЪіРэгЩЃЛШчВЛБфЃЌжБНгаДГіЦфжЕЃЎ
ЕФжмГЄЪЧЗёЗЂЩњБфЛЏЃПШчБфЛЏЃЌМђЪіРэгЩЃЛШчВЛБфЃЌжБНгаДГіЦфжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌ![]() ЮЊ
ЮЊ![]() ЕФжБОЖЃЌЯв
ЕФжБОЖЃЌЯв![]() ЃЌ
ЃЌ![]() ЯрНЛгкЕу
ЯрНЛгкЕу![]() ЃЌЧв
ЃЌЧв![]() гкЕу
гкЕу![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зї
зї![]() ЕФЧаЯпНЛ
ЕФЧаЯпНЛ![]() ЕФбгГЄЯпгкЕу
ЕФбгГЄЯпгкЕу![]() ЃЎ
ЃЎ
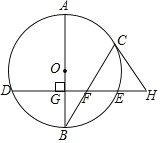
ЃЈ1ЃЉЧѓжЄЃК![]() ЃЛ
ЃЛ
ЃЈ2ЃЉШє![]() ЕФАыОЖЮЊ5ЃЌЕу
ЕФАыОЖЮЊ5ЃЌЕу![]() ЪЧ
ЪЧ![]() ЕФжаЕуЃЌ
ЕФжаЕуЃЌ![]() ЃЌаДГіЧѓЯпЖЮ
ЃЌаДГіЧѓЯпЖЮ![]() ГЄЕФЫМТЗЃЎ
ГЄЕФЫМТЗЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
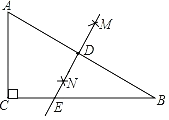
ЁОЬтФПЁПШчЭМЃЌдкЁїABC жаЃЌЁЯACBЃН90ЁуЃЌЗжБ№вдЕуAКЭЕуBЮЊдВаФЃЌвдЯрЭЌЕФГЄЃЈДѓгк![]() ABЃЉЮЊАыОЖзїЛЁЃЌСНЛЁЯрНЛгкЕуMКЭЕуNЃЌзїжБЯпMNНЛABгкЕуDЃЌНЛBCгкЕуEЃЎШєACЃН3ЃЌABЃН5ЃЌдђDEЕШгк_____ЃЎ
ABЃЉЮЊАыОЖзїЛЁЃЌСНЛЁЯрНЛгкЕуMКЭЕуNЃЌзїжБЯпMNНЛABгкЕуDЃЌНЛBCгкЕуEЃЎШєACЃН3ЃЌABЃН5ЃЌдђDEЕШгк_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЩЬЕъЯњЪлвЛжжЩЬЦЗЃЌОЪаГЁЕїВщЗЂЯжЃКИУЩЬЦЗЕФдТЯњЪлСПyЃЈМўЃЉЪЧЪлМлxЃЈдЊ/МўЃЉЕФвЛДЮКЏЪ§ЃЌЦфЪлМлxЁЂдТЯњЪлСПyЁЂдТЯњЪлРћШѓwЃЈдЊЃЉЕФВПЗжЖдгІжЕШчЯТБэЃК
ЪлМлxЃЈдЊ/МўЃЉ | 40 | 45 |
дТЯњЪлСПyЃЈМўЃЉ | 300 | 250 |
дТЯњЪлРћШѓwЃЈдЊЃЉ | 3000 | 3750 |
зЂЃКдТЯњЪлРћШѓЃНдТЯњЪлСПЁСЃЈЪлМлЃНјМлЃЉ
ЃЈ1ЃЉЂйЧѓyЙигкxЕФКЏЪ§БэДяЪНЃЛ
ЂкЕБИУЩЬЦЗЕФЪлМлЪЧЖрЩйдЊЪБЃЌдТЯњЪлРћШѓзюДѓЃПВЂЧѓГізюДѓРћШѓЃЛ
ЃЈ2ЃЉгЩгкФГжждвђЃЌИУЩЬЦЗНјМлЬсИпСЫmдЊ/МўЃЈmЃО0ЃЉЃЌЮяМлВПУХЙцЖЈИУЩЬЦЗЪлМлВЛЕУГЌЙ§40дЊ/МўЃЌИУЩЬЕъдкНёКѓЕФЯњЪлжаЃЌдТЯњЪлСПгыЪлМлШдШЛТњзуЃЈ1ЃЉжаЕФКЏЪ§ЙиЯЕЃЎШєдТЯњЪлзюДѓРћШѓЪЧ2400дЊЃЌдђmЕФжЕЮЊ ЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com