
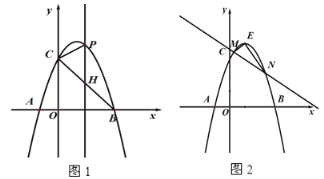
【题目】如图1,已知抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
(1)求![]() ,
,![]() 的值;
的值;
(2)点![]() 是第一象限抛物线上一动点,过点
是第一象限抛物线上一动点,过点![]() 作
作![]() 轴的垂线
轴的垂线![]() ,交
,交![]() 于点
于点![]() .当△
.当△![]() 为等腰三角形时,求点
为等腰三角形时,求点![]() 的坐标;
的坐标;
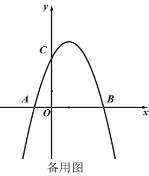
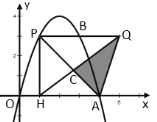
(3)如图2,抛物线顶点为![]() ,已知直线
,已知直线![]() 与二次函数图象相交于
与二次函数图象相交于![]() ,
,![]() 两点.求证:无论
两点.求证:无论![]() 为何值,△
为何值,△![]() 恒为直角三角形.
恒为直角三角形.
【答案】(1)![]() ;(2)点
;(2)点![]() 的坐标
的坐标![]() ,
,![]() ,
,![]() ;(3)见解析.
;(3)见解析.
【解析】
(1)将点![]() 代入解析式中即可求出结论;
代入解析式中即可求出结论;
(2)利用待定系数法求出直线BC的解析式,设点![]() ,则点
,则点 ![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,根据等腰三角形腰的情况分类讨论,然后根据三线合一、等腰直角三角形的性质列出方程即可求出结论;
,根据等腰三角形腰的情况分类讨论,然后根据三线合一、等腰直角三角形的性质列出方程即可求出结论;
(3)将二次函数和一次函数的解析式联立,整理得![]() ,设点
,设点![]() 的坐标为
的坐标为![]() ,根据根与系数的关系可得则
,根据根与系数的关系可得则![]() ,
, ![]()
![]() ,
,![]() ,然后利用平面直角坐标系中任意两点之间的距离公式和勾股定理的逆定理即可证出结论.
,然后利用平面直角坐标系中任意两点之间的距离公式和勾股定理的逆定理即可证出结论.
解:(1)将点![]() 代入
代入![]() ,
,
得![]() ,
,
解得![]() ,
,
∴![]() ;
;
(2)设直线![]() 的解析式为
的解析式为![]() ,
,
将点![]() 代入
代入![]() ,
,
得,![]() ,
,
∴直线![]() 的解析式为
的解析式为![]() ,
,
设点![]() ,则点
,则点 ![]() ,
,
过点![]() 作
作![]() 于点
于点![]() ,
,
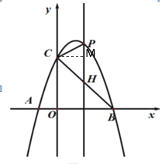
![]()
①当![]() 时,
时,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
即![]() ,
,
解得,![]() (舍去),
(舍去),![]() ,
,
∴![]() ;
;
②当![]() 时,
时,
![]() ,
,
解得![]()
∴![]()
③当![]() 时,此时点P和点M重合
时,此时点P和点M重合
![]() ,
,
解得![]()
∴![]()
综上所述点![]() 的坐标
的坐标![]() ,
,![]() ,
,![]() ;
;
(3)将二次函数与直线![]() 的表达式联立并整理得:
的表达式联立并整理得:![]() ,
,
设点![]() 的坐标为
的坐标为![]() ,
,
则![]() ,
,
则![]()
![]() ,
,
同理:![]() ,
,
点![]() 的坐标为
的坐标为![]() ,
,![]() ,点
,点![]() ,
,
![]()
![]()
![]()
![]()
![]()
![]()
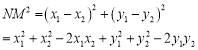
![]()
![]()
![]()
∴![]()
即:![]() 为直角三角形.
为直角三角形.


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:初中数学 来源: 题型:
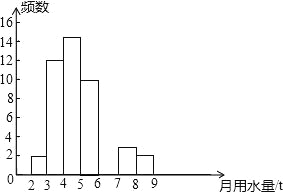
【题目】小亮同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况,他从中随机调查了若干户居民的月均用水量(单位:t),并绘制了样本的频数分布表和频数分布直方图(如图)
月均用水量(单位:t) | 频数 | 百分比 |
2≤x<3 | 2 | 4% |
3≤x<4 | 12 | 24% |
4≤x<5 | a | b |
5≤x<6 | 10 | 20% |
6≤x<7 | c | 12% |
7≤x<8 | 3 | 6% |
8≤x<9 | 2 | 4% |
(1)频数分布表中a= ,b= .(填百分比),c= ;补全频数分布直方图.
(2)如果家庭月均用水量“大于或等于4t且小于7t”为中等用水量家庭,请你通过样本估计总体中的中等用水量家庭大约有 户;
(3)从月均用水量在2≤x<3,8≤x<9这两个范围内的样本家庭中任意抽取2个,请用列表法或画树状图求抽取出的2个家庭来自不同范围的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某旅行团32人在景区A游玩,他们由成人、少年和儿童组成.已知儿童10人,成人比少年多12人.
(1)求该旅行团中成人与少年分别是多少人?
(2)因时间充裕,该团准备让成人和少年(至少各1名)带领10名儿童去另一景区B游玩.景区B的门票价格为100元/张,成人全票,少年8折,儿童6折,一名成人可以免费携带一名儿童.
①若由成人8人和少年5人带队,则所需门票的总费用是多少元?
②若剩余经费只有1200元可用于购票,在不超额的前提下,最多可以安排成人和少年共多少人带队?求所有满足条件的方案,并指出哪种方案购票费用最少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某次数学测验中,一道题满分3分,老师评分只给整数,即得分只能为0分,1分,2分,3分.李老师为了了解学生得分情况和试题的难易情况,对初三(1)班所有学生的试题进行了分析整理,并绘制了两幅尚不完整的统计图,如图所示.

解答下列问题:
(1)m= ,n= ,并补全条形统计图;
(2)在初三(1)班随机抽取一名学生的成绩,求抽中的成绩为得分众数的概率;
(3)根据右侧“小知识”,通过计算判断这道题对于该班级来说,属于哪一类难度的试题?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“新冠肺炎”肆虐,无数抗疫英雄涌现,以下四位抗疫英雄是钟南山、李兰娟、李文亮、张定宇(依次记为![]() ).为让同学们了解四位的事迹,老师设计如下活动:取四张完全相同的卡片,分别写上
).为让同学们了解四位的事迹,老师设计如下活动:取四张完全相同的卡片,分别写上![]() 四个标号,然后背面朝上放置,搅匀后每个同学从中随机抽取一张,记下标号后放回,老师要求每位同学依据抽到的卡片上的标号查找相应抗疫英雄的资料,并做成小报.
四个标号,然后背面朝上放置,搅匀后每个同学从中随机抽取一张,记下标号后放回,老师要求每位同学依据抽到的卡片上的标号查找相应抗疫英雄的资料,并做成小报.

(1)班长在四种卡片中随机抽到标号为![]() 的概率为_______.
的概率为_______.
(2)平平和安安两位同学抽到的卡片是不同英雄的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 上有一点
上有一点![]() ,
,![]() 的横坐标为1,过
的横坐标为1,过![]() 作
作![]() 轴,与抛物线的另一个交点为
轴,与抛物线的另一个交点为![]() ,且
,且![]() ,作
,作![]() 轴,垂足为
轴,垂足为![]() ,抛物线与
,抛物线与![]() 轴正半轴交于点
轴正半轴交于点![]() ,连结
,连结![]() ,
,![]() 与
与![]() 交于点
交于点![]() .
.
(1)当![]() 时,①求点
时,①求点![]() 的坐标:②求
的坐标:②求![]() 的面积:
的面积:
(2)当![]() 是以
是以![]() 为腰的等腰三角形时,求
为腰的等腰三角形时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点到直线的距离即为点到直线的垂线段的长.

(1)如图1,取点M(1,0),则点M到直线l:y=![]() x﹣1的距离为多少?
x﹣1的距离为多少?
(2)如图2,点P是反比例函数y=![]() 在第一象限上的一个点,过点P分别作PM⊥x轴,作PN⊥y轴,记P到直线MN的距离为d0,问是否存在点P,使d0=
在第一象限上的一个点,过点P分别作PM⊥x轴,作PN⊥y轴,记P到直线MN的距离为d0,问是否存在点P,使d0=![]() ?若存在,求出点P的坐标,若不存在,请说明理由.
?若存在,求出点P的坐标,若不存在,请说明理由.
(3)如图3,若直线y=kx+m与抛物线y=x2﹣4x相交于x轴上方两点A、B(A在B的左边).且∠AOB=90°,求点P(2,0)到直线y=kx+m的距离最大时,直线y=kx+m的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,D、E分别在边AB、AC上,下列条件中,不能确定△ADE∽△ACB的是( )
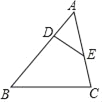
A. ∠AED=∠B B. ∠BDE+∠C=180°
C. ADBC=ACDE D. ADAB=AEAC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了落实国务院的指示精神,某地方政府出台了一系列“三农”优惠政策,使农民收入大幅度增加.某农户生产经销一种农产品,已知这种产品的成本价为每千克20元,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)有如下关系:y=﹣2x+80.设这种产品每天的销售利润为w元.
(1)求w与x之间的函数关系式.
(2)该产品销售价定为每千克多少元时,每天的销售利润最大?最大利润是多少元?
(3)如果物价部门规定这种产品的销售价不高于每千克28元,该农户想要每天获得150元的销售利润,销售价应定为每千克多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com