
【题目】如图,抛物线![]() 上有一点
上有一点![]() ,
,![]() 的横坐标为1,过
的横坐标为1,过![]() 作
作![]() 轴,与抛物线的另一个交点为
轴,与抛物线的另一个交点为![]() ,且
,且![]() ,作
,作![]() 轴,垂足为
轴,垂足为![]() ,抛物线与
,抛物线与![]() 轴正半轴交于点
轴正半轴交于点![]() ,连结
,连结![]() ,
,![]() 与
与![]() 交于点
交于点![]() .
.
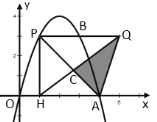
(1)当![]() 时,①求点
时,①求点![]() 的坐标:②求
的坐标:②求![]() 的面积:
的面积:
(2)当![]() 是以
是以![]() 为腰的等腰三角形时,求
为腰的等腰三角形时,求![]() 的值.
的值.
【答案】(1)①![]() ;②
;②![]() ;(2)3或
;(2)3或![]()
【解析】
(1)将![]() 代入解析式,先求得P点坐标,再由对称轴求得B点坐标,由
代入解析式,先求得P点坐标,再由对称轴求得B点坐标,由![]() 即可求出Q的坐标;根据图象中的相似三角形可得出
即可求出Q的坐标;根据图象中的相似三角形可得出![]() 的值,由
的值,由![]() 的面积可求得
的面积可求得![]() 的面积;
的面积;
(2)先由解析式得出相关点的坐标,用含b的代数式表示线段的长,当![]() 是以
是以![]() 为腰的等腰三角形时,分两类情况:
为腰的等腰三角形时,分两类情况:![]() 或
或![]() ,分情况求解即可.
,分情况求解即可.
解:(1)①当![]() 时,
时,![]() ,抛物线的对称轴为直线
,抛物线的对称轴为直线![]() ,
,
∵![]() 的横坐标为1,
的横坐标为1,
将![]() 代入
代入![]() ,得:
,得:![]() ,
,
∴点![]() 的坐标为
的坐标为![]() ,
,
∵![]() 轴,与抛物线的另一个交点为
轴,与抛物线的另一个交点为![]() ,
,![]() ,
,
∴点![]() 与点B关于直线
与点B关于直线![]() 对称,则点
对称,则点![]() 的坐标为
的坐标为![]() ,
,
∴![]() ,则
,则![]() ,
,
∴点![]() 的横坐标为 5,
的横坐标为 5,
∴点![]() 的坐标为
的坐标为![]() ;
;
②令![]() ,即
,即![]() ,
,
解得:![]() ,
,
∴点![]() 的坐标为
的坐标为![]() ,
,
∵![]() 轴,
轴,
∴点![]() 的坐标为
的坐标为![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() 的面积∶
的面积∶![]() 的面积
的面积![]() ,
,
则![]() 的面积∶
的面积∶![]() 的面积
的面积![]() ,
,
∵![]() 的面积
的面积![]() ,
,
∴![]() 的面积
的面积![]() ;
;
(2)由![]() ,得
,得![]() ,抛物线的对称轴为直线
,抛物线的对称轴为直线![]() ,
,
∴![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,
![]() ,
,
令![]() ,即
,即![]() ,
,
解得:![]() ,
,
∴点![]() 的坐标为
的坐标为![]() ,
,
![]() ,则
,则![]() ,
,
∵![]() ,
,
∴![]() 为等腰直角三角形,
为等腰直角三角形,
∴![]() ,
,
∵![]() 轴
轴
∴![]()
当![]() 是以
是以![]() 为腰的等腰三角形时,则有
为腰的等腰三角形时,则有![]() 或
或![]() ,
,
①当![]() 时,则
时,则![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]()
由![]() 得:
得:![]() ,
,
解得:![]() ;
;
②当![]() 时,
时,
在![]() 中,
中,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
解得:![]()
综上所述,当![]() 是以
是以![]() 为腰的等腰三角形时,
为腰的等腰三角形时,![]() 的值为3或
的值为3或![]() .
.


 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:
【题目】在某次训练中,甲、乙两名射击运动员各射击10发子弹的成绩统计图如图所示,对于本次训练,有如下结论:①S甲2>S乙2;②S甲2<S乙2;③甲的射击成绩比乙稳定;④乙的射击成绩比甲稳定,由统计图可知正确的结论是( )
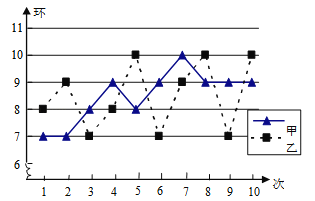
A.①③ B.①④ C.②③ D.②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC的平分线AD与边BC的垂直平分线ED相交于点D,过点D作DF⊥AC交AC延长线于点F,若AB=8,AC=4,则CF的长为_________.
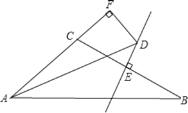
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
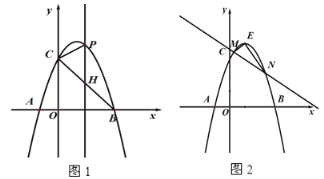
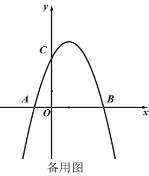
(1)求![]() ,
,![]() 的值;
的值;
(2)点![]() 是第一象限抛物线上一动点,过点
是第一象限抛物线上一动点,过点![]() 作
作![]() 轴的垂线
轴的垂线![]() ,交
,交![]() 于点
于点![]() .当△
.当△![]() 为等腰三角形时,求点
为等腰三角形时,求点![]() 的坐标;
的坐标;
(3)如图2,抛物线顶点为![]() ,已知直线
,已知直线![]() 与二次函数图象相交于
与二次函数图象相交于![]() ,
,![]() 两点.求证:无论
两点.求证:无论![]() 为何值,△
为何值,△![]() 恒为直角三角形.
恒为直角三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
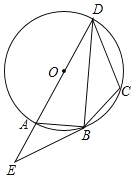
【题目】如图,四边形ABCD的外接圆为⊙O,AD是⊙O的直径,过点B作⊙O的切线,交DA的延长线于点E,连接BD,且∠E=∠DBC.
(1)求证:DB平分∠ADC;
(2)若CD=9,tan∠ABE=![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
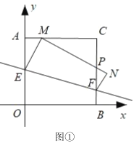
【题目】将一个正方形纸片![]() 放置在平面直角坐标系中,点
放置在平面直角坐标系中,点![]() ,点
,点![]() ,
,![]() ,
,![]() 点.动点
点.动点![]() 在边
在边![]() 上,点
上,点![]() 在边
在边![]() 上,沿
上,沿![]() 折叠该纸片,使点
折叠该纸片,使点![]() 的对应点
的对应点![]() 始终落在边
始终落在边![]() 上(点
上(点![]() 不与
不与![]() 重合),点
重合),点![]() 落在点
落在点![]() 处,
处,![]() 与
与![]() 交于点
交于点![]() .
.
(Ⅰ)如图①,当![]() 时,求点
时,求点![]() 的坐标;
的坐标;
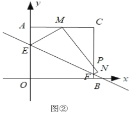
(Ⅱ)如图②,当点![]() 落在
落在![]() 的中点时,求点
的中点时,求点![]() 的坐标;
的坐标;
(Ⅲ)随着点![]() 在
在![]() 边上位置的变化,
边上位置的变化,![]() 的周长是否发生变化?如变化,简述理由;如不变,直接写出其值.
的周长是否发生变化?如变化,简述理由;如不变,直接写出其值.
查看答案和解析>>
科目:初中数学 来源: 题型:
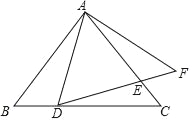
【题目】已知:如图,在△ABC中,点D、E分别在边BC、AC上,点F在DE的延长线上,AD=AF,AECE=DEEF.
(1)求证:△ADE∽△ACD;
(2)如果AEBD=EFAF,求证:AB=AC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a,b,c 为常数,且a≠0)的图像上部分点的横坐标x和纵
坐标y的对应值如下表
x | … | -1 | 0 | 1 | 2 | 3 | … |
y | … | -3 | -3 | -1 | 3 | 9 | … |
关于x的方程ax2+bx+c=0一个负数解x1满足k<x1<k+1(k为整数),则k=________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com