
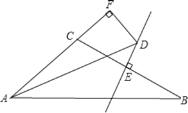
【题目】如图,在△ABC中,∠BAC的平分线AD与边BC的垂直平分线ED相交于点D,过点D作DF⊥AC交AC延长线于点F,若AB=8,AC=4,则CF的长为_________.
【答案】![]()
【解析】
连接CD,DB,过点D作DM⊥AB于点M,证明△AFD≌△AMD,得到AF=AM,FD=DM,证明Rt△CDF≌Rt△BDM,得到BM=CF,结合图形计算,得到答案.
如图,连接CD,DB,过点D作DM⊥AB于点M,
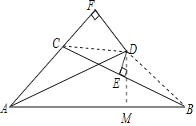
∵AD平分∠FAB,
∴∠FAD=∠DAM,
在△AFD和△AMD中,
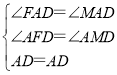 ,
,
∴△AFD≌△AMD(AAS)
∴AF=AM,FD=DM,
∵DE垂直平分BC
∴CD=BD,
在Rt△CDF和Rt△BDM中,
![]() ,
,
∴Rt△CDF≌Rt△BDM(HL)
∴BM=CF,
∵AB=AM+BM=AF+MB=AC+CF+MB=AC+2CF,
∴8=4+2CF,
解得,CF=2,
故答案为:2.


 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:初中数学 来源: 题型:
【题目】如图所示,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 由点
由点![]() 出发沿
出发沿![]() 方向向点
方向向点![]() 匀速运动,同时点
匀速运动,同时点![]() 由点
由点![]() 出发沿
出发沿![]() 方向向点
方向向点![]() 匀速运动,它们的速度均为
匀速运动,它们的速度均为![]() .连接
.连接![]() ,设运动时间为
,设运动时间为![]() .
.
(1)当![]() 为何值时,
为何值时,![]() ?
?
(2)设![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 的函数关系式,并求出当
的函数关系式,并求出当![]() 为何值时,
为何值时,![]() 取得最大值?
取得最大值?![]() 的最大值是多少?
的最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
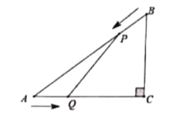
【题目】据交管部门统计,高速公路超速行驶是引发交通事故的主要原因.我县某校数学课外小组的几个同学想尝试用自己所学的知识检测车速,渝黔高速公路某路段的限速是:每小时80千米(即最高时速不超过80千米),如图,他们将观测点设在到公路l的距离为0.1千米的P处.这时,一辆轿车由綦江向重庆匀速直线驶来,测得此车从A处行驶到B处所用的时间为3秒(注:3秒=![]() 小时),并测得∠APO=59°,∠BPO=45°.试计算AB并判断此车是否超速?(精确到0.001).(参考数据:sin59°≈0.8572,cos59°≈0.5150,tan59°≈1.6643)
小时),并测得∠APO=59°,∠BPO=45°.试计算AB并判断此车是否超速?(精确到0.001).(参考数据:sin59°≈0.8572,cos59°≈0.5150,tan59°≈1.6643)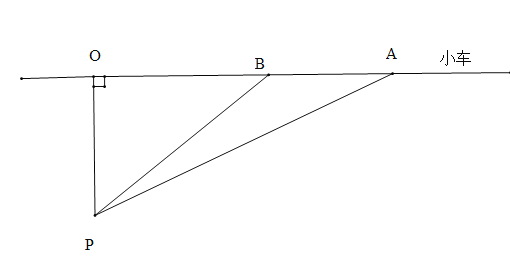
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】桃花中学计划购买![]() 两种型号的小黑板,经洽谈, 购买一块
两种型号的小黑板,经洽谈, 购买一块![]() 型小黑板比买一块
型小黑板比买一块![]() 型小黑板多
型小黑板多![]() 元,且购买
元,且购买![]() 块
块![]() 型小黑板和
型小黑板和![]() 块
块![]() 型小黑板共需
型小黑板共需![]() 元.
元.
(1)求购买一块![]() 型小黑板和一块
型小黑板和一块![]() 型小黑板各需要多少元?
型小黑板各需要多少元?
(2)根据学校的实际情况,需购买![]() 两种型号的小黑板共
两种型号的小黑板共![]() 块,并且购买
块,并且购买![]() 型小黑板的数量不少于购买
型小黑板的数量不少于购买![]() 型小黑板的数量,请问学校购买这批小黑板最少要多少元?
型小黑板的数量,请问学校购买这批小黑板最少要多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某旅行团32人在景区A游玩,他们由成人、少年和儿童组成.已知儿童10人,成人比少年多12人.
(1)求该旅行团中成人与少年分别是多少人?
(2)因时间充裕,该团准备让成人和少年(至少各1名)带领10名儿童去另一景区B游玩.景区B的门票价格为100元/张,成人全票,少年8折,儿童6折,一名成人可以免费携带一名儿童.
①若由成人8人和少年5人带队,则所需门票的总费用是多少元?
②若剩余经费只有1200元可用于购票,在不超额的前提下,最多可以安排成人和少年共多少人带队?求所有满足条件的方案,并指出哪种方案购票费用最少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1所示,以点M(1,0)为圆心的圆与y轴,x轴分别交于点A,B,C,D,与⊙M相切于点H的直线EF交x轴于点E(![]() ,0),交y轴于点F(0,
,0),交y轴于点F(0,![]() ).
).
(1)求⊙M的半径r;
(2)如图2所示,连接CH,弦HQ交x轴于点P,若cos∠QHC=![]() ,求
,求![]() 的值;
的值;
(3)如图3所示,点P为⊙M上的一个动点,连接PE,PF,求PF+![]() PE的最小值.
PE的最小值.
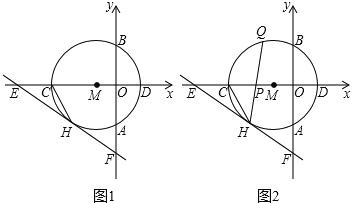
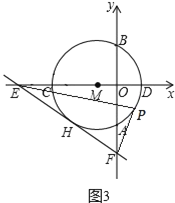
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某次数学测验中,一道题满分3分,老师评分只给整数,即得分只能为0分,1分,2分,3分.李老师为了了解学生得分情况和试题的难易情况,对初三(1)班所有学生的试题进行了分析整理,并绘制了两幅尚不完整的统计图,如图所示.

解答下列问题:
(1)m= ,n= ,并补全条形统计图;
(2)在初三(1)班随机抽取一名学生的成绩,求抽中的成绩为得分众数的概率;
(3)根据右侧“小知识”,通过计算判断这道题对于该班级来说,属于哪一类难度的试题?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 上有一点
上有一点![]() ,
,![]() 的横坐标为1,过
的横坐标为1,过![]() 作
作![]() 轴,与抛物线的另一个交点为
轴,与抛物线的另一个交点为![]() ,且
,且![]() ,作
,作![]() 轴,垂足为
轴,垂足为![]() ,抛物线与
,抛物线与![]() 轴正半轴交于点
轴正半轴交于点![]() ,连结
,连结![]() ,
,![]() 与
与![]() 交于点
交于点![]() .
.
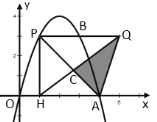
(1)当![]() 时,①求点
时,①求点![]() 的坐标:②求
的坐标:②求![]() 的面积:
的面积:
(2)当![]() 是以
是以![]() 为腰的等腰三角形时,求
为腰的等腰三角形时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
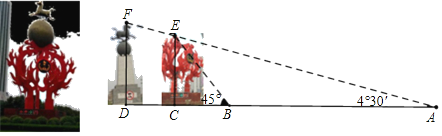
【题目】“马踏飞燕”作为商丘的地标性雕塑被拆分为两座雕塑,安放在紧邻高速公路出站口的平原路和华商大道交叉口,不光临近古城景区,也靠近火神台,恰恰实现了商丘市的城市文化宣传的目的.“人们来到商丘,一下高速,就看到商丘的地标,就能够感受到商丘的火文化.”
某中学数学兴趣小组准备测量安放后的雕塑相关数据,如图,小明从A点测得“火球”最高点E的仰角为4°30′,此处恰好看不到“马踏飞燕”雕塑的最高点F,小明向雕塑走140m到达点B,此时测得点E的仰角为45°.已知两雕塑的距离为50m,求两座雕塑EC、FD的高度.(A、B、C、D在同一直线上)(精确到1m,参考值:sin4°30′≈0.07,cos4°30′≈0.99,tan4°30′≈0.08.)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com