练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】二次函数y＝ax2＋bx＋c（a，b，c 为常数，且a≠0）的图像上部分点的横坐标x和纵

    坐标y的对应值如下表

    x

    …

    －1

    0

    1

    2

    3

    …

    y

    …

    －3

    －3

    －1

    3

    9

    …

    关于x的方程ax2＋bx＋c＝0一个负数解x1满足k＜x1＜k+1（k为整数），则k＝________．

    【答案】－3

    【解析】

    首先利用表中的数据求出二次函数，再利用求根公式解得x1，再利用夹逼法可确定x1的取值范围，可得k．

    解:把x=0,y=-3,x=1,y=-1,x=-1,y=-3代入y＝ax2＋bx＋c得

    ，解得，∴y=x+x-3,

    ∵△=b2-4ac=12-4×1×（-3）=13，
    ∴x==1±，
    ∵<0,

    ∴=1-＜0，
    ∵-4≤-≤-3，
    ∴，
    ∴-3≤1≤，
    ∵整数k满足k＜x1＜k+1，
    ∴k=-3，
    故答案为:-3．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，抛物线上有一点，的横坐标为1，过作轴，与抛物线的另一个交点为，且，作轴，垂足为，抛物线与轴正半轴交于点，连结，与交于点．

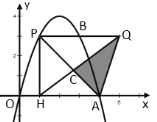
    （1）当时，①求点的坐标：②求的面积：

    （2）当是以为腰的等腰三角形时，求的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】“马踏飞燕”作为商丘的地标性雕塑被拆分为两座雕塑，安放在紧邻高速公路出站口的平原路和华商大道交叉口，不光临近古城景区，也靠近火神台，恰恰实现了商丘市的城市文化宣传的目的．“人们来到商丘，一下高速，就看到商丘的地标，就能够感受到商丘的火文化．”

    某中学数学兴趣小组准备测量安放后的雕塑相关数据，如图，小明从A点测得“火球”最高点E的仰角为4°30′，此处恰好看不到“马踏飞燕”雕塑的最高点F，小明向雕塑走140m到达点B，此时测得点E的仰角为45°．已知两雕塑的距离为50m，求两座雕塑EC、FD的高度．（A、B、C、D在同一直线上）（精确到1m，参考值：sin4°30′≈0.07，cos4°30′≈0.99，tan4°30′≈0.08．）

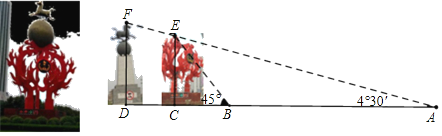
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某社区调查社区居民双休日的学习状况，采取下列调查方式：①从一幢高层住宅楼中选取200名居民；②从不同住层楼中随机选取200名居民；③选取社区内的200名在校学生．

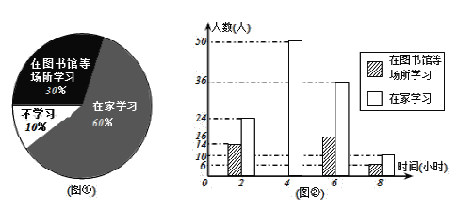
    （1）上述调查方式最合理的是　 　（填序号）；

    （2）将最合理的调查方式得到的数据制成扇形统计图（如图①）和频数分布直方图（如图②）．

    ①请补全直方图（直接画在图②中）；

    ②在这次调查中，200名居民中，在家学习的有　 　人；

    （3）请估计该社区2000名居民中双休日学习时间不少于4h的人数；

    （4）小明的叔叔住在该社区，那么双休日他去叔叔家时，正好叔叔没有学习的概率是　 　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了落实国务院的指示精神，某地方政府出台了一系列“三农”优惠政策，使农民收入大幅度增加．某农户生产经销一种农产品，已知这种产品的成本价为每千克20元，市场调查发现，该产品每天的销售量y（千克）与销售价x（元/千克）有如下关系：y=﹣2x+80．设这种产品每天的销售利润为w元．

    （1）求w与x之间的函数关系式．

    （2）该产品销售价定为每千克多少元时，每天的销售利润最大？最大利润是多少元？

    （3）如果物价部门规定这种产品的销售价不高于每千克28元，该农户想要每天获得150元的销售利润，销售价应定为每千克多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知二次函数y＝x2－2mx＋m2＋m－1（m为常数）．

    （1）求证：不论m为何值，该二次函数的图像与x轴总有两个公共点；

    （2）将该二次函数的图像向下平移k（k＞0）个单位长度，使得平移后的图像经过点（0，－2），则k的取值范围是 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，是的对角线，，的边，，的长是三个连续偶数，，分别是边，上的动点，且，将沿着折叠得到，连接，．若为直角三角形时，的长为_______．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

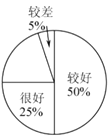
    【题目】我国北方又进入了火灾多发季节，为此，某校在全校1200名学生中随机抽取一部分人进行“安全防火，警钟长鸣”知识问卷调查活动，对问卷调查成绩按“很好”、“较好”、“一般”“较差”四类汇总分析，并绘制了如下扇形统计图和条形统计图．

    （1）本次活动共抽取了多少名同学？

    （2）补全条形统计图；

    （3）根据以上调查结果分析，估计该校1200名学生中，对“安全防火”知识了解“较好”和“很好”的学生大约共计有多少名．

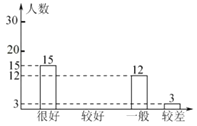
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系中，抛物线：沿轴翻折得到抛物线.

    （1）求抛物线的顶点坐标；

    （2）横、纵坐标都是整数的点叫做整点．

    ① 当时，求抛物线和围成的封闭区域内(包括边界)整点的个数；

    ② 如果抛物线C1和C2围成的封闭区域内(包括边界)恰有个整点，求m取值范围．

    查看答案和解析>>

    同步练习册答案