
【题目】已知二次函数y=x2-2![]() mx+m2+m-1(m为常数).
mx+m2+m-1(m为常数).
(1)求证:不论m为何值,该二次函数的图像与x轴总有两个公共点;
(2)将该二次函数的图像向下平移k(k>0)个单位长度,使得平移后的图像经过点(0,-2),则k的取值范围是 .
【答案】(1)证明见解析;(2)k≥![]() .
.
【解析】
(1)根据判别式的值得到△=(2m-1)2 +3>0,然后根据判别式的意义得到结论;
(2)把(0,-2)带入平移后的解析式,利用配方法得到k= (m+![]() )+
)+![]() ,即可得出结果.
,即可得出结果.
(1)证:当y=0时 x2-2![]() mx+m2+m-1=0
mx+m2+m-1=0
∵b2-4ac=(-2![]() m)2-4(m2+m-1)
m)2-4(m2+m-1)
=8m2-4m2-4m+4
=4m2-4m+4
=(2m-1)2 +3>0
∴方程x2-2![]() mx+m2+m-1=0有两个不相等的实数根
mx+m2+m-1=0有两个不相等的实数根
∴二次函数y=x2-2![]() mx+m2+m-1图像与x轴有两个公共点
mx+m2+m-1图像与x轴有两个公共点
(2)解:平移后的解析式为: y=x2-2![]() mx+m2+m-1-k,过(0,-2),
mx+m2+m-1-k,过(0,-2),
∴-2=0-0+m+m-1-k, ∴k= m+m+1=(m+![]() )+
)+![]() ,∴k≥
,∴k≥![]() .
.


 特高级教师点拨系列答案
特高级教师点拨系列答案科目:初中数学 来源: 题型:
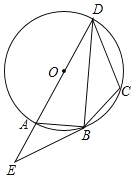
【题目】如图,四边形ABCD的外接圆为⊙O,AD是⊙O的直径,过点B作⊙O的切线,交DA的延长线于点E,连接BD,且∠E=∠DBC.
(1)求证:DB平分∠ADC;
(2)若CD=9,tan∠ABE=![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,点D、E分别在边BC和AB上,且AD=AC,EB=ED,分别延长ED、AC交于点F.

(1)求证:△ABD∽△FDC;
(2)求证:AE2=BEEF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠BAC=90°,AB=AC,AD⊥BC于点D.
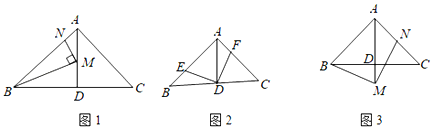
(1)如图1,点M,N分别在AD,AB上,且∠BMN=90°,当∠AMN=30°,AB=2时,求线段AM的长;
(2)如图2,点E,F分别在AB,AC上,且∠EDF=90°,求证:BE=AF;
(3)如图3,点M在AD的延长线上,点N在AC上,且∠BMN=90°,求证:AB+AN=![]() AM.
AM.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a,b,c 为常数,且a≠0)的图像上部分点的横坐标x和纵
坐标y的对应值如下表
x | … | -1 | 0 | 1 | 2 | 3 | … |
y | … | -3 | -3 | -1 | 3 | 9 | … |
关于x的方程ax2+bx+c=0一个负数解x1满足k<x1<k+1(k为整数),则k=________.
查看答案和解析>>
科目:初中数学 来源: 题型:
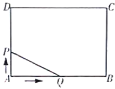
【题目】如图,矩形![]() 的周长是
的周长是![]() ,且
,且![]() 比
比![]() 长
长![]() .若点
.若点![]() 从点
从点![]() 出发,以
出发,以![]() 的速度沿
的速度沿![]() 方向匀速运动,同时点
方向匀速运动,同时点![]() 从点
从点![]() 出发,以
出发,以![]() 的速度沿
的速度沿![]() 方向匀速运动,当一个点到达点
方向匀速运动,当一个点到达点![]() 时,另一个点也随之停止运动.若设运动时间为
时,另一个点也随之停止运动.若设运动时间为![]() ,
,![]() 的面积为
的面积为![]() ,则
,则![]() 与
与![]() 之间的函数图象大致是( )
之间的函数图象大致是( )
A.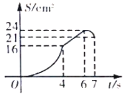 B.
B.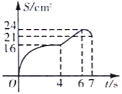
C.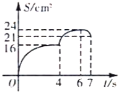 D.
D.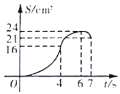
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】河南灵宝苹果为中华苹果之翘楚,被誉为“中华名果”.某水果超市计划从灵宝购进“红富士”与“新红星”两种品种的苹果.已知2箱红富士苹果的进价与3箱新红星苹果的进价的和为282元,且每箱红富士苹果的进价比每箱新红星苹果的进价贵6元.
(1)求每箱红富士苹果的进价与每箱新红星苹果的进价分别是多少元?
(2)如果购进红富士苹果有优惠,优惠方案是:购进红富士苹果超过20箱,超出部分可以享受七折优惠.若购进![]() (
(![]() ,且
,且![]() 为整数)箱红富士苹果需要花费
为整数)箱红富士苹果需要花费![]() 元,求
元,求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)在(2)的条件下,超市决定在红富士、新红星两种苹果中选购其中一种,且数量超过20箱,请你帮助超市选择购进哪种苹果更省钱.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是我国古代数学的经典著作,书中有一个问题:“今有黄金九枚,白银一十一枚,称之重适等.交易其一,金轻十三两.问金、银一枚各重几何?”.意思是:甲袋中装有黄金9枚(每枚黄金重量相同),乙袋中装有白银11枚(每枚白银重量相同),称重两袋相等.两袋互相交换1枚后,甲袋比乙袋轻了13两(袋子重量忽略不计).问黄金、白银每枚各重多少两?设每枚黄金重x两,每枚白银重y两,根据题意得( )
A. ![]()
B. ![]()
C. ![]()
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,∠ABD=90°,延长AB至点E,使BE=AB,连接CE.
(1)求证:四边形BECD是矩形;
(2)连接DE交BC于点F,连接AF,若CE=2,∠DAB=30°,求AF的长.
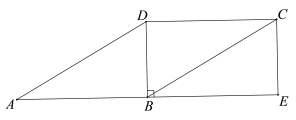
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com