
【题目】在证明等腰三角形的判定定理“等角对等边”,即“如图,已知:∠B=∠C,求证:AB=AC”时,小明作了如下的辅助线,下列对辅助线的描述正确的有( )
①作∠BAC的平分线AD交BC于点D②取BC边的中点D,连接AD③过点A作AD⊥BC,垂足为点D④作BC边的垂直平分线AD,交BC于点D
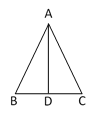
A.1个B.2个C.3个D.4个
科目:初中数学 来源: 题型:
【题目】一幅长20cm、宽12cm的图案,如图,其中有一横两竖的彩条,横、竖彩条的宽度比为3:2.设竖彩条的宽度为xcm,图案中三条彩条所占面积为ycm2.
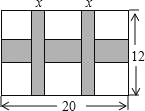
(1)求y与x之间的函数关系式;
(2)若图案中三条彩条所占面积是图案面积的![]() ,求横、竖彩条的宽度.
,求横、竖彩条的宽度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班为了解学生一学期做义工的时间情况,对全班50名学生进行调查,按做义工的时间![]() (单位:小时),将学生分成五类:
(单位:小时),将学生分成五类: ![]() 类(
类(![]() ),
),![]() 类(
类(![]() ),
),![]() 类(
类(![]() ),
),![]() 类(
类(![]() ),
),![]() 类(
类(![]() ),绘制成尚不完整的条形统计图如图11.
),绘制成尚不完整的条形统计图如图11.

根据以上信息,解答下列问题:
(1)![]() 类学生有 人,补全条形统计图;
类学生有 人,补全条形统计图;
(2)![]() 类学生人数占被调查总人数的 %;
类学生人数占被调查总人数的 %;
(3)从该班做义工时间在![]() 的学生中任选2人,求这2人做义工时间都在
的学生中任选2人,求这2人做义工时间都在![]() 中的概率.
中的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某旅行团32人在景区A游玩,他们由成人、少年和儿童组成.已知儿童10人,成人比少年多12人.
(1)求该旅行团中成人与少年分别是多少人?
(2)因时间充裕,该团准备让成人和少年(至少各1名)带领10名儿童去另一景区B游玩.景区B的门票价格为100元/张,成人全票,少年8折,儿童6折,一名成人可以免费携带一名儿童.
①若由成人8人和少年5人带队,则所需门票的总费用是多少元?
②若剩余经费只有1200元可用于购票,在不超额的前提下,最多可以安排成人和少年共多少人带队?求所有满足条件的方案,并指出哪种方案购票费用最少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“勤劳”是中华民族的传统美德,学校要求同学们在家里帮助父母做一些力所能及的家务.在本学期开学初,小颖同学随机调查了部分同学寒假在家做家务的总时间,设被调查的每位同学寒假在家做家务的总时间为x小时,将做家务的总时间分为五个类别:A(0≤x<10),B(10≤x<20),C(20≤x<30),D(30≤x<40),E(x≥40).并将调查结果制成如下两幅不完整的统计图:
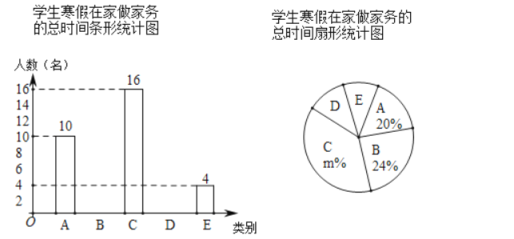
根据统计图提供的信息,解答下列问题:
(1)本次共调查了 名学生;
(2)请根据以上信息直接在答题卡中补全条形统计图;
(3)扇形统计图中m的值是 ,类别D所对应的扇形圆心角的度数是 度;
(4)若该校有800名学生,根据抽样调查的结果,请你估计该校有多少名学生寒假在家做家务的总时间不低于20小时.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某次数学测验中,一道题满分3分,老师评分只给整数,即得分只能为0分,1分,2分,3分.李老师为了了解学生得分情况和试题的难易情况,对初三(1)班所有学生的试题进行了分析整理,并绘制了两幅尚不完整的统计图,如图所示.

解答下列问题:
(1)m= ,n= ,并补全条形统计图;
(2)在初三(1)班随机抽取一名学生的成绩,求抽中的成绩为得分众数的概率;
(3)根据右侧“小知识”,通过计算判断这道题对于该班级来说,属于哪一类难度的试题?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“新冠肺炎”肆虐,无数抗疫英雄涌现,以下四位抗疫英雄是钟南山、李兰娟、李文亮、张定宇(依次记为![]() ).为让同学们了解四位的事迹,老师设计如下活动:取四张完全相同的卡片,分别写上
).为让同学们了解四位的事迹,老师设计如下活动:取四张完全相同的卡片,分别写上![]() 四个标号,然后背面朝上放置,搅匀后每个同学从中随机抽取一张,记下标号后放回,老师要求每位同学依据抽到的卡片上的标号查找相应抗疫英雄的资料,并做成小报.
四个标号,然后背面朝上放置,搅匀后每个同学从中随机抽取一张,记下标号后放回,老师要求每位同学依据抽到的卡片上的标号查找相应抗疫英雄的资料,并做成小报.

(1)班长在四种卡片中随机抽到标号为![]() 的概率为_______.
的概率为_______.
(2)平平和安安两位同学抽到的卡片是不同英雄的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点到直线的距离即为点到直线的垂线段的长.

(1)如图1,取点M(1,0),则点M到直线l:y=![]() x﹣1的距离为多少?
x﹣1的距离为多少?
(2)如图2,点P是反比例函数y=![]() 在第一象限上的一个点,过点P分别作PM⊥x轴,作PN⊥y轴,记P到直线MN的距离为d0,问是否存在点P,使d0=
在第一象限上的一个点,过点P分别作PM⊥x轴,作PN⊥y轴,记P到直线MN的距离为d0,问是否存在点P,使d0=![]() ?若存在,求出点P的坐标,若不存在,请说明理由.
?若存在,求出点P的坐标,若不存在,请说明理由.
(3)如图3,若直线y=kx+m与抛物线y=x2﹣4x相交于x轴上方两点A、B(A在B的左边).且∠AOB=90°,求点P(2,0)到直线y=kx+m的距离最大时,直线y=kx+m的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
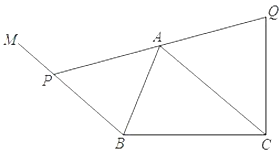
【题目】已知:如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() .过点
.过点![]() 作
作![]() ,动点
,动点![]() 在射线
在射线![]() 上(点
上(点![]() 不与
不与![]() 重合),联结
重合),联结![]() 并延长到点
并延长到点![]() ,使
,使![]() .
.
(1)求![]() 的面积;
的面积;
(2)设![]() ,
,![]() ,求
,求![]() 关于
关于![]() 的函数解析式,并写出
的函数解析式,并写出![]() 的取值范围;
的取值范围;
(3)连接![]() ,如果
,如果![]() 是直角三角形,求
是直角三角形,求![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com