
科目: 来源: 题型:
【题目】定义:我们把关于某一点成中心对称的两条抛物线叫“孪生抛物线”;(1)已知抛物线L:y=﹣x2+4与x轴交于A、B两点(A在B的左侧),与y轴交于C点,求L关于坐标原点O(0,0)的“孪生抛物线”W;(2)点N为坐标平面内一点,且△BCN是以BC为斜边的等腰直角三角形,在x轴是否存在一点M(m,0),使抛物线L关于点M的“孪生抛物线”过点N,如果存在,求出M点坐标;不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,P为⊙O直径AB延长线上的一点,PC切⊙O于点C,过点B作CP的垂线BH交⊙O于点D,连结AC,CD.
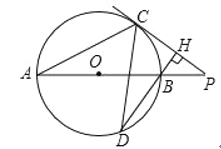
(1)求证:∠PBH=2∠HDC;
(2)若sin∠P=![]() ,BH=3,求BD的长.
,BH=3,求BD的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,某数学活动小组选定测量小河对岸大树BC的高度,他们在斜坡上D处测得大树顶端B的仰角是30°,朝大树方向下坡走6米到达坡底A处,在A处测得大树顶端B的仰角是45°,若坡角∠FAE=30°,求大树的高度(结果保留根号).
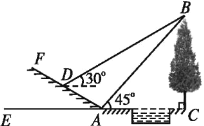
查看答案和解析>>
科目: 来源: 题型:
【题目】小昕的口袋中有5把相似的钥匙,其中2把钥匙(记为A1,A2)能打开教室前门锁,而剩余的3把钥匙(记为B1,B2,B3)不能打开教室前门锁.
(1)小昕从口袋中随便摸出一把钥匙就能打开教室前门锁的概率是 ;
(2)请用树状图或列表等方法,求出小昕从口袋中第一次随机摸出的一把钥匙不能打开教室前门锁(摸出的钥匙不再放回),而第二次随机摸出的一把钥匙正好能打开教室前门锁的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】一名在校大学生利用“互联网+”自主创业,销售一种产品,这种产品的成本价10元/件,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于16元/件,市场调查发现,该产品每天的销售量![]() (件
(件![]() 与销售价
与销售价![]() (元/件)之间的函数关系如图所示.
(元/件)之间的函数关系如图所示.
(1)求![]() 与
与![]() 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(2)求每天的销售利润W(元![]() 与销售价
与销售价![]() (元/件)之间的函数关系式,并求出每件销售价为多少元时,每天的销售利润最大?最大利润是多少?
(元/件)之间的函数关系式,并求出每件销售价为多少元时,每天的销售利润最大?最大利润是多少?

查看答案和解析>>
科目: 来源: 题型:
【题目】去年4月,过敏体质检测中心等机构开展了青少年形体测评,专家组随机抽查了某市若干名初中生坐姿、站姿、走姿的好坏情况.我们对专家的测评数据作了适当处理(如果一个学生有一种以上不良姿势,我们以他最突出的一种作记载),并将统计结果绘制成了如下两幅不完整的统计图,请你根据图中所给信息解答些列问题:
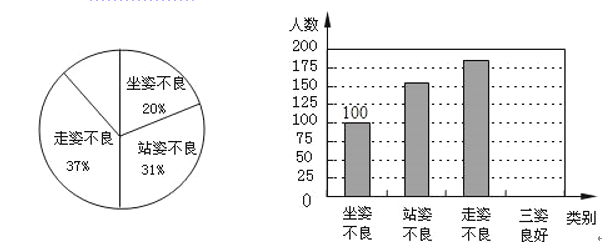
(1)请将两幅图补充完整;
(2)如果全市有10万名初中生,那么全市初中生中,三姿良好的学生约有 人.
(3)根据统计结果,请你简单谈谈自己的看法.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,将△ABC沿BC边上的中线AD平移到△A′B′C′的位置,已知△ABC的面积为18,阴影部分三角形的面积为8,若AA′=1,则A′D的值为______.
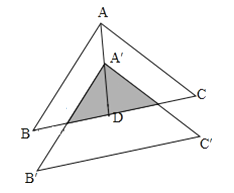
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,点A在双曲线y=![]() 上,点B在双曲线y=
上,点B在双曲线y=![]() (k≠0)上,AB∥x轴,过点A作AD⊥x轴于D.连接OB,与AD相交于点C,若AC=2CD,则k=__.
(k≠0)上,AB∥x轴,过点A作AD⊥x轴于D.连接OB,与AD相交于点C,若AC=2CD,则k=__.
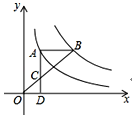
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,抛物线![]() (
(![]() )的顶点为
)的顶点为![]() ,对称轴与
,对称轴与![]() 轴交于点
轴交于点![]() ,当以
,当以![]() 为对角线的正方形
为对角线的正方形![]() 的另外两个顶点
的另外两个顶点![]() 、
、![]() 恰好在抛物线上时,我们把这样的抛物线称为美丽抛物线,正方形
恰好在抛物线上时,我们把这样的抛物线称为美丽抛物线,正方形![]() 为它的内接正方形.
为它的内接正方形.
(1)当抛物线![]() 是美丽抛物线时,则
是美丽抛物线时,则![]() ______;当抛物线
______;当抛物线![]() 是美丽抛物线时,则
是美丽抛物线时,则![]() ______;
______;
(2)若抛物线![]() 是美丽抛物线时,则请直接写出
是美丽抛物线时,则请直接写出![]() ,
,![]() 的数量关系;
的数量关系;
(3)若![]() 是美丽抛物线时,(2)
是美丽抛物线时,(2)![]() ,
,![]() 的数量关系成立吗?为什么?
的数量关系成立吗?为什么?
(4)系列美丽抛物线![]() (
(![]() 为小于
为小于![]() 的正整数)顶点在直线
的正整数)顶点在直线![]() 上,且它们中恰有两条美丽抛物线内接正方形面积比为
上,且它们中恰有两条美丽抛物线内接正方形面积比为![]() .求它们二次项系数之和.
.求它们二次项系数之和.
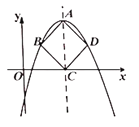
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com