
科目: 来源: 题型:
【题目】如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.

(1)求证:AF=DC;
(2)若AB⊥AC,试判断四边形ADCF的形状,并证明你的结论.
查看答案和解析>>
科目: 来源: 题型:
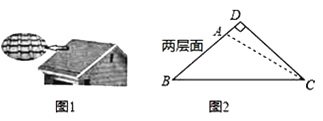
【题目】太阳能光伏建筑是现代绿色环保建筑之一,老张准备把自家屋顶改建成光伏瓦面,改建前屋顶截面△ABC如图2所示,BC=10米,∠ABC=∠ACB=36°,改建后顶点D在BA的延长线上,且∠BDC=90°,求改建后南屋面边沿增加部分AD的长.(结果精确到0.1米)
(参考数据:sin18°≈0.31,cos18°≈0.95.tan18°≈0.32,sin36°≈0.59.cos36°≈0.81,tan36°≈0.73)
查看答案和解析>>
科目: 来源: 题型:
【题目】请用学过的方法研究一类新函数![]() (
(![]() 为常数,
为常数,![]() )的图象和性质.
)的图象和性质.
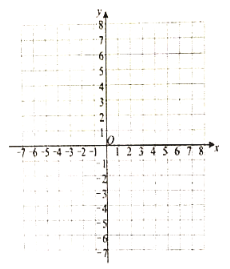
(1)在给出的平面直角坐标系中画出函数![]() 的图象;
的图象;
(2)对于函数![]() ,当自变量
,当自变量![]() 的值增大时,函数值
的值增大时,函数值![]() 怎样变化?
怎样变化?
查看答案和解析>>
科目: 来源: 题型:
【题目】2019年5月,以“寻根国学,传承文明”为主题的兰州市第三届“国学少年强一国学知识挑战赛”总决赛拉开帷幕,小明晋级了总决赛.比赛过程分两个环节,参赛选手须在每个环节中各选择一道题目.
第一环节:写字注音、成语故事、国学常识、成语接龙(分别用![]() 表示);
表示);
第二环节:成语听写、诗词对句、经典通读(分别用![]() 表示)
表示)
(1)请用树状图或列表的方法表示小明参加总决赛抽取题目的所有可能结果
(2)求小明参加总决赛抽取题目都是成语题目(成语故事、成语接龙、成语听写)的概率。
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,动点
,动点![]() 从点
从点![]() 出发,沿
出发,沿![]() 方向匀速运动,速度为
方向匀速运动,速度为![]() ;同时,动点
;同时,动点![]() 从点
从点![]() 出发,沿
出发,沿![]() 方向匀速运动,速度为
方向匀速运动,速度为![]() ;当一个点停止运动,另一个点也停止运动.设点
;当一个点停止运动,另一个点也停止运动.设点![]() ,
,![]() 运动的时间是
运动的时间是![]()
![]()
![]() .过点
.过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() .
.
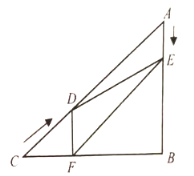
(1)![]() 为何值时,
为何值时,![]() ?
?
(2)设四边形![]() 的面积为
的面积为![]() ,试求出
,试求出![]() 与
与![]() 之间的关系式;
之间的关系式;
(3)是否存在某一时刻![]() ,使得
,使得![]() 若存在,求出
若存在,求出![]() 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
(4)当![]() 为何值时,
为何值时,![]() ?
?
查看答案和解析>>
科目: 来源: 题型:
【题目】空间任意选定一点![]() ,以点
,以点![]() 为端点,作三条互相垂直的射线
为端点,作三条互相垂直的射线![]() ,
,![]() ,
,![]() .这三条互相垂直的射线分别称作
.这三条互相垂直的射线分别称作![]() 轴、
轴、![]() 轴、
轴、![]() 轴,统称为坐标轴,它们的方向分别为
轴,统称为坐标轴,它们的方向分别为![]() (水平向前),
(水平向前),![]() (水平向右),
(水平向右),![]() (竖直向上)方向,这样的坐标系称为空间直角坐标系.将相邻三个面的面积记为
(竖直向上)方向,这样的坐标系称为空间直角坐标系.将相邻三个面的面积记为![]() ,
,![]() ,
,![]() ,且
,且![]() 的小长方体称为单位长方体,现将若干个单位长方体在空间直角坐标系内进行码放,要求码放时将单位长方体
的小长方体称为单位长方体,现将若干个单位长方体在空间直角坐标系内进行码放,要求码放时将单位长方体![]() 所在的面与
所在的面与![]() 轴垂直,
轴垂直,![]() 所在的面与
所在的面与![]() 轴垂直,
轴垂直,![]() 所在的面与
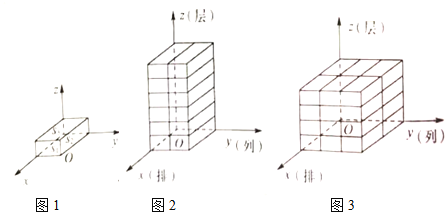
所在的面与![]() 轴垂直,如图1所示.若将
轴垂直,如图1所示.若将![]() 轴方向表示的量称为几何体码放的排数,
轴方向表示的量称为几何体码放的排数,![]() 轴方向表示的量称为几何体码放的列数,二轴方向表示的量称为几何体码放的层数;如图2是由若干个单位长方体在空间直角坐标内码放的一个几何体,其中这个几何体共码放了
轴方向表示的量称为几何体码放的列数,二轴方向表示的量称为几何体码放的层数;如图2是由若干个单位长方体在空间直角坐标内码放的一个几何体,其中这个几何体共码放了![]() 排
排![]() 列
列![]() 层,用有序数组记作
层,用有序数组记作![]() ,如图3的几何体码放了
,如图3的几何体码放了![]() 排
排![]() 列
列![]() 层,用有序数组记作
层,用有序数组记作![]() .这样我们就可用每一个有序数组
.这样我们就可用每一个有序数组![]() 表示一种几何体的码放方式.
表示一种几何体的码放方式.
(1)有序数组![]() 所对应的码放的几何体是______________;
所对应的码放的几何体是______________;
A.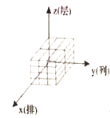 B.
B.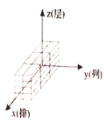 C.
C.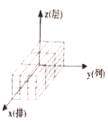 D.
D.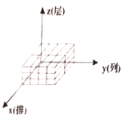
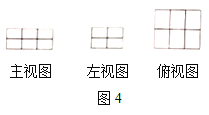
(2)图4是由若干个单位长方体码放的一个几何体的三视图,则这种码放方式的有序数组为(______,_______,_______),组成这个几何体的单位长方体的个数为____________个.
(3)为了进一步探究有序数组![]() 的几何体的表面积公式
的几何体的表面积公式![]() ,某同学针对若干个单位长方体进行码放,制作了下列表格:
,某同学针对若干个单位长方体进行码放,制作了下列表格:
几何体有序数组 | 单位长方体的个数 | 表面上面积为S1的个数 | 表面上面积为S2的个数 | 表面上面积为S3的个数 | 表面积 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
根据以上规律,请直接写出有序数组![]() 的几何体表面积
的几何体表面积![]() 的计算公式;(用
的计算公式;(用![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 表示)
表示)
(4)当![]() ,
,![]() ,
,![]() 时,对由
时,对由![]() 个单位长方体码放的几何体进行打包,为了节约外包装材料,我们可以对
个单位长方体码放的几何体进行打包,为了节约外包装材料,我们可以对![]() 个单位长方体码放的几何体表面积最小的规律进行探究,请你根据自己探究的结果直接写出使几何体表面积最小的有序数组,这个有序数组为(______,_______, ______),此时求出的这个几何体表面积的大小为____________(缝隙不计)
个单位长方体码放的几何体表面积最小的规律进行探究,请你根据自己探究的结果直接写出使几何体表面积最小的有序数组,这个有序数组为(______,_______, ______),此时求出的这个几何体表面积的大小为____________(缝隙不计)
查看答案和解析>>
科目: 来源: 题型:
【题目】交通工程学理论把在单向道路上行驶的汽车看成连续的流体,并用流量、速度、密度三个概念描述车流的基本特征,其中流量![]() (辆
(辆![]() 小时)指单位时间内通过道路指定断面的车辆数;速度
小时)指单位时间内通过道路指定断面的车辆数;速度![]() (千米
(千米![]() 小时)指通过道路指定断面的车辆速度,密度
小时)指通过道路指定断面的车辆速度,密度![]() (辆
(辆![]() 千米)指通过道路指定断面单位长度内的车辆数.为配合大数据治堵行动,测得某路段流量
千米)指通过道路指定断面单位长度内的车辆数.为配合大数据治堵行动,测得某路段流量![]() 与速度
与速度![]() 之间关系的部分数据如下表:
之间关系的部分数据如下表:
速度v(千米/小时) |
|
|
|
|
|
|
|
|
流量q(辆/小时) |
|
|
|
|
|
|
|
|
(1)根据上表信息,下列三个函数关系式中,刻画![]() ,
,![]() 关系最准确是_____________________.(只填上正确答案的序号)
关系最准确是_____________________.(只填上正确答案的序号)
①![]() ;②
;②![]() ;③
;③![]()
(2)请利用(1)中选取的函数关系式分析,当该路段的车流速度为多少时,流量达到最大?最大流量是多少?
(3)已知![]() ,
,![]() ,
,![]() 满足
满足![]() ,请结合(1)中选取的函数关系式继续解决下列问题:市交通运行监控平台显示,当
,请结合(1)中选取的函数关系式继续解决下列问题:市交通运行监控平台显示,当![]() 时道路出现轻度拥堵.试分析当车流密度
时道路出现轻度拥堵.试分析当车流密度![]() 在什么范围时,该路段将出现轻度拥堵?
在什么范围时,该路段将出现轻度拥堵?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.

(1)求证:AF=DC;
(2)若AB⊥AC,试判断四边形ADCF的形状,并证明你的结论.
查看答案和解析>>
科目: 来源: 题型:
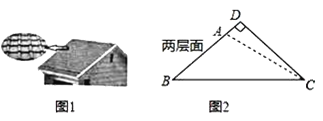
【题目】太阳能光伏建筑是现代绿色环保建筑之一,老张准备把自家屋顶改建成光伏瓦面,改建前屋顶截面△ABC如图2所示,BC=10米,∠ABC=∠ACB=36°,改建后顶点D在BA的延长线上,且∠BDC=90°,求改建后南屋面边沿增加部分AD的长.(结果精确到0.1米)
(参考数据:sin18°≈0.31,cos18°≈0.95.tan18°≈0.32,sin36°≈0.59.cos36°≈0.81,tan36°≈0.73)
查看答案和解析>>
科目: 来源: 题型:
【题目】请用学过的方法研究一类新函数![]() (
(![]() 为常数,
为常数,![]() )的图象和性质.
)的图象和性质.
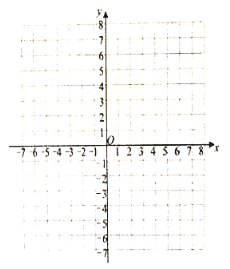
(1)在给出的平面直角坐标系中画出函数![]() 的图象;
的图象;
(2)对于函数![]() ,当自变量
,当自变量![]() 的值增大时,函数值
的值增大时,函数值![]() 怎样变化?
怎样变化?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com