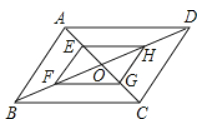
A.EH=HGB.四边形EFGH是平行四边形

C.AC⊥BDD.的面积是的面积的2倍

A. BE=DF B. AE=CF C. AF//CE D. ∠BAE=∠DCF

【题目】如图1，是内任意一点，连接，分别以为边作（在的左侧）和（在的右侧），使得，，连接．

（1）求证：；

（2）如图2，交于点，若，点共线，其他条件不变，

①判断四边形的形状，并说明理由；

②当，，且四边形是正方形时，直接写出的长．

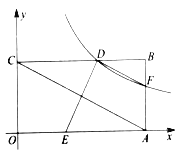
【题目】如图，在平面直角坐标系中，矩形的顶点分别在轴和轴的正半轴上，顶点的坐标为（4,2），的垂直平分线分别交于点，过点的反比例函数的图像交于点．

（1）求反比例函数的表示式；

（2）判断与的位置关系，并说明理由；

（3）连接，在反比例函数图像上存在点，使，直接写出点的坐标．

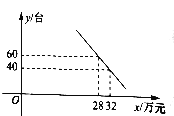
【题目】为促进新旧功能转换，提高经济效益，某科技公司近期研发出一种新型高科技设备，每台设备成本价为25万元，经过市场调研发现，该设备的月销售量（台）和销售单价（万元）满足如图所示的一次函数关系．

（1）求月销售量与销售单价的函数关系式；

（2）根据相关规定，此设备的销售单价不得高于35万元，如果该公司想获得130万元的月利润，那么该设备的销售单价应是多少万元？

【题目】为了“城市更美好、人民更幸福”，我市开展“三城联创”活动，环卫部门要求垃圾按三类分别装袋、投放，其中类指废电池，过期药品等有毒垃圾，类指剩余食品等厨余垃圾，类指塑料、废纸等可回收垃圾，甲、乙两人各投放一袋垃圾．

（1）甲投放的垃圾恰好是类的概率是 ；

（2）用树状图或表格求甲、乙两人投放的垃圾是不同类别的概率．

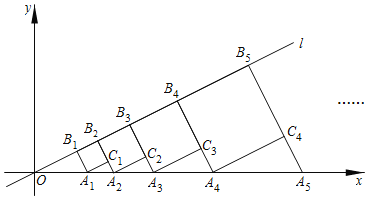
【题目】如图，点在直线上，点的横坐标为，过作，交轴于点，以为边，向右作正方形，延长交轴于点；以为边，向右作正方形，延长交轴于点；以为边，向右作正方形延长交轴于点；按照这个规律进行下去，点的横坐标为_____（结果用含正整数的代数式表示）

【题目】如图，抛物线经过三点

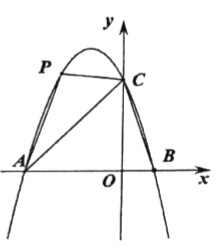
（1）求抛物线的解析式；

（2）在直线上方的抛物线上是否存在一点，使的面积等于的面积的一半？若存在，求出点的坐标；若不存在，说明理由；

（3）点为抛物线上一动点，在轴上是否存在点，使以，，，为顶点的四边形是平行四边形？若存在，求出点的坐标；若不存在，请说明理由．

【题目】如图，以的边上一点为圆心的圆，经过，两点，且与边交于点，为弧的中点，连接交于，，连接.

（1）求证：是的切线；

（2）已知的半径，，求的面积.

(1)若平行于墙的一边长为y米，直接写出y与x的函数关系式及其自变量x的取值范围.

(2)垂直于墙的一边的长为多少米时，这个苗圃园的面积最大，并求出这个最大值.